Diofantske - Primjer 5
Riješiti jednadžbu u skupu prirodnih brojeva: 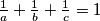 .
.
Rješenje:
Intuicija iza rješenja je da ne smiju sva tri broja  istovremeno biti velika. Ako
istovremeno biti velika. Ako 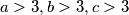 onda imamo da je izraz na lijevoj strani manji od jedan. Bez smanjenja opštosti, pretpostavimo
onda imamo da je izraz na lijevoj strani manji od jedan. Bez smanjenja opštosti, pretpostavimo 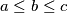 što smijemo jer je jednadžba simetrična u ove tri varijable (kada zamijenimo uloge
što smijemo jer je jednadžba simetrična u ove tri varijable (kada zamijenimo uloge 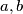 sa
sa 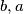 jednadžba se ne mijenja). Zaključujemo da
jednadžba se ne mijenja). Zaključujemo da 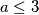 jer je najmanji od tri varijable. Sada razlikujemo tri slučaja:
jer je najmanji od tri varijable. Sada razlikujemo tri slučaja:
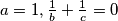 kontradikcija.
kontradikcija.
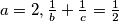 . Odavdje slično radimo kao na početku:
. Odavdje slično radimo kao na početku:  i
i  ne mogu biti istovremeno veći od
ne mogu biti istovremeno veći od  . Opet bez smanjenja opštosti,
. Opet bez smanjenja opštosti, 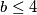 . Slučaj
. Slučaj  nema rješenja, preostala dva imaju
nema rješenja, preostala dva imaju 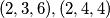 .
.
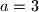 . Ovdje
. Ovdje 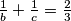 . Bez smanjenja opštosti
. Bez smanjenja opštosti 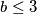 odakle imamo jedno rješenje
odakle imamo jedno rješenje 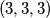 .
.
Dakle, sva rješenja su 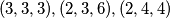 te njihove permutacije (zbog inicijalne pretpostavke za usmjerenje
te njihove permutacije (zbog inicijalne pretpostavke za usmjerenje  ).
).
Za rješenje upišite 5
