Površine - Uvod
Dobrodošli na 3. tjedan MetaMath tečaja! Ovaj ćemo tjedan posvetiti proučavanju zadataka s površinama. Više materijala možete pronaći u ovom odličnom MNM predavanju. Počnimo naš tjedan pregledom najpoznatijih formula za površinu trokuta.
Površinu trokuta možemo izračunati:
1. Preko jedne stranice i visine na nju
Vjerujem da svi znamo najpoznatiju formulu za površinu trokuta,  Gdje je
Gdje je  stranica trokuta, a
stranica trokuta, a 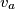 visina na nju.
visina na nju.
2. Preko svih stranica i radijusa upisane kružnice
Površinu trokuta možemo izračunati ako znamo duljine svih stranica trokuta:  i radijus upisane kružnice
i radijus upisane kružnice  formulom
formulom  gdje
gdje  označava poluopseg
označava poluopseg 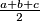
3. Preko svih stranica i radijusa opisane kružnice
Ako pak znamo duljine svih stranica trokuta:  i radijus opisane kružnice
i radijus opisane kružnice  površinu možemo izračunati formulom
površinu možemo izračunati formulom 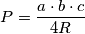
4. Preko dvije stranice i kuta između njih
Ako znamo duljine dviju stranica trokuta: 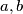 i kut između njih
i kut između njih  uz pomoć malo trigonometrije površinu dobijamo formulom
uz pomoć malo trigonometrije površinu dobijamo formulom 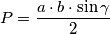
5. Preko svih stranica
Ako znamo duljine svih stranica trokuta  možemo iskoristiti Heronovu formulu da izračunamo površinu:
možemo iskoristiti Heronovu formulu da izračunamo površinu: 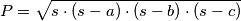 gdje
gdje  označava poluopseg.
označava poluopseg.
Kao rješenje upišite broj formula za površinu koje smo naveli u ovom uvodu.
