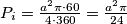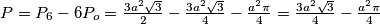Prvi tip zadatka s površinama koji ćemo upoznati često se pojavljuje na županijskom natjecanju, a zahtjeva od nas da izračunamo površinu osjenčenog dijela nekog lika.
Zadatak: Izračunajte površinu šrafiranog lika na slici ako stranica pravilnog šesterokuta ima duljinu a.
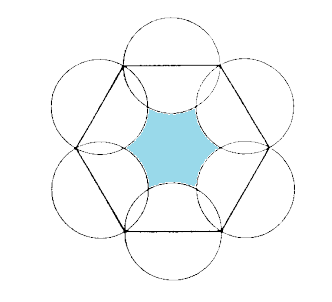
Rješenje: 1. korak: Što zapravo moramo izračunati? Kod ovakvih zadataka, najbolja je strategija podijeliti lik na elemente kojima znamo izračunati površinu. Zapitajmo se koji su to likovi?
Za početak, znamo formulu za površinu šesterokuta: 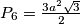 .
.
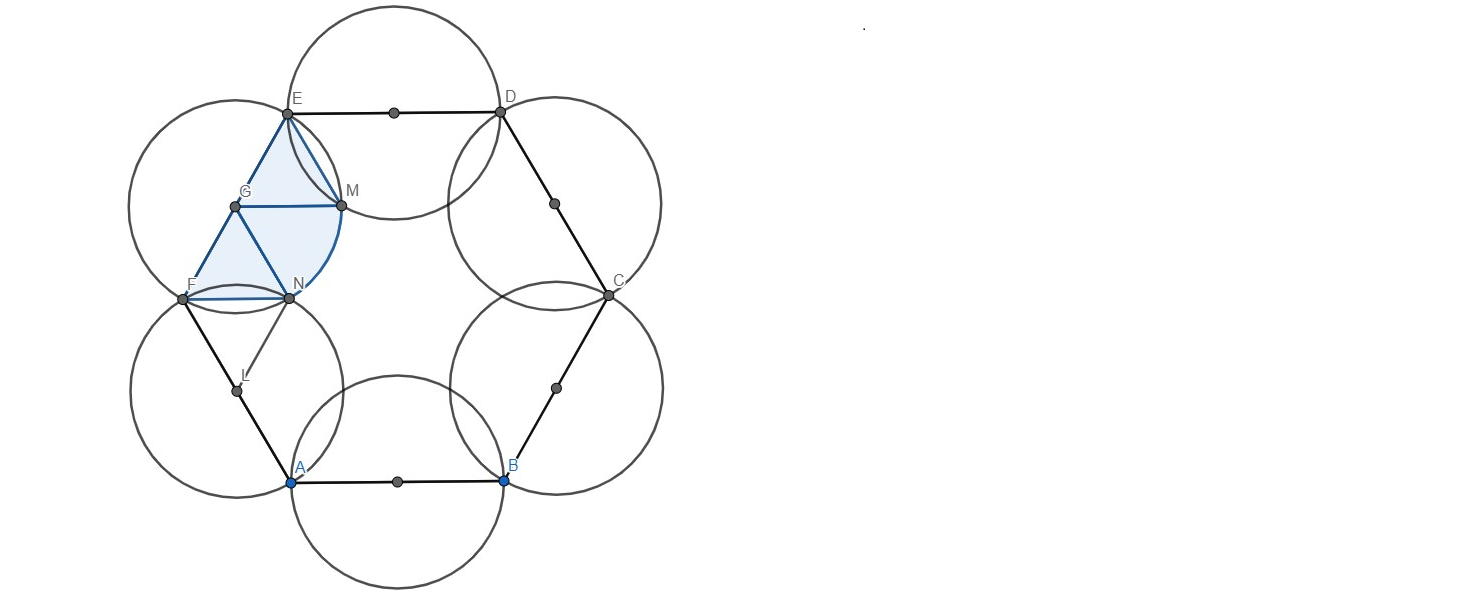
Vidimo da površinu šrafiranog lika možemo dobiti kao razliku površine šesterokuta i šest površina označenih na slici.
2. korak: Računanje površine šest manjih likova
Čini nam se da računanje površine označenog lika vodi k rješenju, pa je označimo s 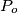 i nastavljamo dijeliti lik na djelove kojima znamo izračunati površinu.
i nastavljamo dijeliti lik na djelove kojima znamo izračunati površinu.
Vidimo da se lik sastoji od  sukladna trokuta i kružnog isječka. Nadalje, zbog simetrije trokuti su sukladni, a lako dokazujemo da su i jednakostranični. Naime, mjera kuta
sukladna trokuta i kružnog isječka. Nadalje, zbog simetrije trokuti su sukladni, a lako dokazujemo da su i jednakostranični. Naime, mjera kuta 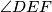 je
je 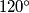 jer je to unutarnji kut šesterokuta, dakle zbog simetrije
jer je to unutarnji kut šesterokuta, dakle zbog simetrije 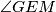 je točno pola,
je točno pola, 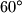 . Kako su
. Kako su 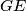 i
i 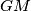 radijusi, riječ je o jednakokračnom trokutu kojemu je jedan kut
radijusi, riječ je o jednakokračnom trokutu kojemu je jedan kut 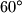 , dakle jednakostraničnom trokutu.
, dakle jednakostraničnom trokutu.
Dakle, lik se sastoji od:
1. 2 jednakostranična trokuta stranice 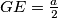 . Njihova površina je
. Njihova površina je 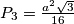
2. Jednog kružnog isječka Lako je vidjeti da je središnji kut kružnog isječka 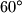 , a radijus kružnica
, a radijus kružnica 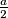 , pa je površina
, pa je površina 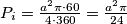
Vidimo da je površina osjenčenih likova 
2. korak: Računanje površine šarafa
Konačno, tražena površina je 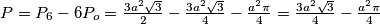
Kao rješenje upišite "saraf"
Prvi tip zadatka s površinama koji ćemo upoznati često se pojavljuje na županijskom natjecanju, a zahtjeva od nas da izračunamo površinu osjenčenog dijela nekog lika.
\textbf{Zadatak:} Izračunajte površinu šrafiranog lika na slici ako stranica pravilnog šesterokuta ima duljinu a.
\\
\includegraphics{sl1.png}
\\
\textbf{Rješenje:}
\textbf{1. korak: Što zapravo moramo izračunati?}
Kod ovakvih zadataka, najbolja je strategija podijeliti lik na elemente kojima znamo izračunati površinu. Zapitajmo se koji su to likovi?
Za početak, znamo formulu za površinu šesterokuta: $P_{6} = \frac{3a^2\sqrt{3}}{2}$.
\\
\includegraphics{sl2.png}
\\
Vidimo da površinu šrafiranog lika možemo dobiti kao razliku površine šesterokuta i šest površina označenih na slici.
\textbf{2. korak: Računanje površine šest manjih likova}
Čini nam se da računanje površine označenog lika vodi k rješenju, pa je označimo s $P_o$ i nastavljamo dijeliti lik na djelove kojima znamo izračunati površinu.
Vidimo da se lik sastoji od $2$ sukladna trokuta i kružnog isječka. Nadalje, zbog simetrije trokuti su sukladni, a lako dokazujemo da su i jednakostranični. Naime, mjera kuta $\angle{DEF}$ je $120^\circ$ jer je to unutarnji kut šesterokuta, dakle zbog simetrije $\angle{GEM}$ je točno pola, $60^\circ$. Kako su $GE$ i $GM$ radijusi, riječ je o jednakokračnom trokutu kojemu je jedan kut $60^\circ$, dakle jednakostraničnom trokutu.
Dakle, lik se sastoji od: \\
1. 2 jednakostranična trokuta stranice $GE = \frac{a}2$.
Njihova površina je $P_3 = \frac{a^2\sqrt{3}}{16}$ \\
2. Jednog kružnog isječka
Lako je vidjeti da je središnji kut kružnog isječka $60^\circ$, a radijus kružnica $\frac a2$, pa je površina
$P_i = \frac{a^2 \pi \cdot 60}{4 \cdot 360}= \frac{ a^2 \pi}{24}$
Vidimo da je površina osjenčenih likova $P_o = 2\cdot P_3+P_i = \frac{a^2\sqrt{3}}{8} + \frac{ a^2\pi}{24}$
\textbf{2. korak: Računanje površine šarafa}
Konačno, tražena površina je
$P = P_6 - 6P_o = \frac{3a^2\sqrt{3}}{2}- \frac{3a^2\sqrt{3}}{4} - \frac{a^2\pi}{4}= \frac{3a^2\sqrt{3}}{4} - \frac{a^2\pi}{4}$
\\
\\
Kao rješenje upišite "saraf"

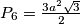 .
. 
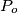 i nastavljamo dijeliti lik na djelove kojima znamo izračunati površinu.
i nastavljamo dijeliti lik na djelove kojima znamo izračunati površinu. sukladna trokuta i kružnog isječka. Nadalje, zbog simetrije trokuti su sukladni, a lako dokazujemo da su i jednakostranični. Naime, mjera kuta
sukladna trokuta i kružnog isječka. Nadalje, zbog simetrije trokuti su sukladni, a lako dokazujemo da su i jednakostranični. Naime, mjera kuta 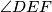 je
je 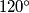 jer je to unutarnji kut šesterokuta, dakle zbog simetrije
jer je to unutarnji kut šesterokuta, dakle zbog simetrije 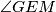 je točno pola,
je točno pola, 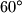 . Kako su
. Kako su 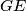 i
i 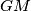 radijusi, riječ je o jednakokračnom trokutu kojemu je jedan kut
radijusi, riječ je o jednakokračnom trokutu kojemu je jedan kut 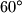 , dakle jednakostraničnom trokutu.
, dakle jednakostraničnom trokutu.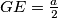 . Njihova površina je
. Njihova površina je 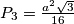
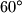 , a radijus kružnica
, a radijus kružnica 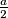 , pa je površina
, pa je površina