MetaMath '23

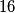Mnogi se zadaci mogu riješiti tako što se izjednače dvije različite formule za površinu. \textbf{Zadatak:} Unutar trokuta $ABC$ nalaze se točke $S$ i $T$. Udaljenosti točke $S$ od pravaca $AB$, $BC$ i $CA$ su redom $10$, $7$ i $4$. Udaljenosti točke $T$ od tih pravaca su redom $4$, $10$ i $16$. Odredi polumjer trokutu $ABC$ upisane kružnice. \textbf{Rješenje:} Polumjer ćemo odrediti prikazujući površinu preko poluopsega, zatim primjenjujući formulu za površinu preko polumjera upisane kružnice i poluopsega da dobijemo traženi radijus. \textbf{1. 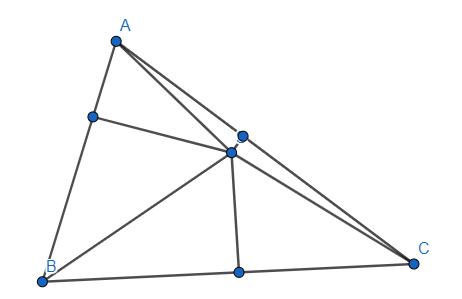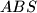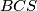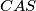korak: Površina trokuta $\triangle ABC$ preko $S$} \\ \includegraphics{00s.png} \\ Primijetimo da je zbroj površina trokuta $ABS$, $BCS$ i $CAS$ jednak površini $ABC$. Raspisujemo:\\ $\begin{aligned}P_{ABC} &= P_{ABS} + P_{BCS} + P_{CAS} \\ &= \frac{c\cdot 10}{2} + \frac{a\cdot 7}{2} + \frac{b\cdot 4}2 \end{aligned}$ \\ Iz čega je 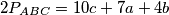$2P_{ABC} = 10c + 7a + 4b$ \textbf{2. 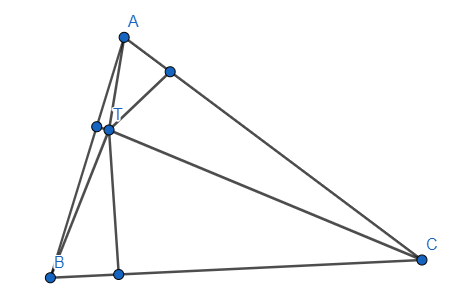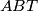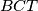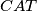korak: Površina trokuta $\triangle ABC$ preko $T$} \\ \includegraphics{00t.png} \\ Analogno, primijetimo da je zbroj površina trokuta $ABT$, $BCT$ i $CAT$ jednak površini $ABC$. 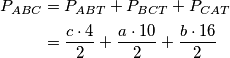Raspisujemo: \\ $\begin{aligned}P_{ABC} &= P_{ABT} + P_{BCT} + P_{CAT} \\ &= \frac{c\cdot 4}{2} + \frac{a\cdot 10}{2} + \frac{b\cdot 16}2 \end{aligned}$\\ Iz čega je 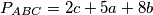$P_{ABC} = 2c + 5a + 8b$ \textbf{3. 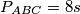korak: poluopseg $s$} Zbrajanjem prikaza površine iz prvog i drugog koraka dobijamo $$3P_{ABC} = 12c+12a+12b = 12 \cdot 2 s = 24 s$$ Zato je $P_{ABC} = 8s$ \textbf{4. 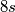korak: računanje polumjera} Kako znamo da je površina trokuta $ABC$ jednaka $r\cdot s$, ali također i $8s$, zaključujemo da je traženi polumjer $8$. \\ \\ Kao rješenje upišite "ST".