Često je u zadacima s površinom, pogotovo u onima u kojima se pojavljuju četverokuti, korisno razmišljati o Talesovom poučku i omjerima.
Zadatak: Točke  i
i  leže na stranici
leže na stranici  pravokutnika
pravokutnika  tako da vrijedi
tako da vrijedi 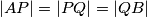 . Pravac
. Pravac 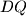 siječe pravce
siječe pravce  i
i 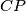 redom u točkama
redom u točkama  i
i  , a pravac
, a pravac 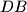 siječe pravce
siječe pravce  i
i 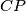 redom u točkama
redom u točkama  i
i  . Odredite omjer površina četverokuta
. Odredite omjer površina četverokuta 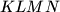 i pravokutnika
i pravokutnika  .
.
Rješenje:
1. korak: Formula za površinu 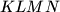
Primijetimo da zbog simetrije vrijedi 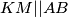 i
i 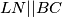 , stoga su dijagonale četverokuta
, stoga su dijagonale četverokuta 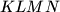 okomite. To znači da je površina četverokuta
okomite. To znači da je površina četverokuta 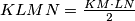 . Sada nam cilj postaje odrediti omjer
. Sada nam cilj postaje odrediti omjer 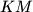 i
i  , te
, te 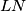 i
i  . Označimo
. Označimo 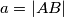 i
i 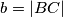 .
.
2. korak: Računanje visine trokuta 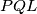
Za početak, primijetimo da su trokuti 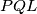 i
i 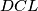 slični, te da im je koeficijent sličnosti
slični, te da im je koeficijent sličnosti 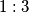 (jer je
(jer je 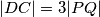 ). To znači da je visina trokuta
). To znači da je visina trokuta 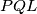 jednaka trećini visine
jednaka trećini visine 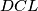 . Jasno je da je zbroj te
. Jasno je da je zbroj te  visine
visine  , stoga je
, stoga je 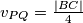 .
.
3. korak: Računanje 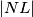
Lako je vidjeti da su trokuti 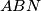 i
i 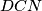 sukladni, te da im je zbroj visina jednak
sukladni, te da im je zbroj visina jednak  - zato su im visine
- zato su im visine 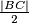 . Zbog paralelnosti
. Zbog paralelnosti 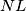 i
i  , dužinu
, dužinu 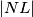 možemo prikazati kao razliku duljina visina
možemo prikazati kao razliku duljina visina 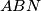 i
i 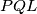 .
.
Zbog toga, 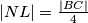 .
.
4. korak: Računanje visine trokuta 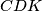
Primijetimo tako da su trokuti 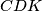 i
i 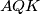 slični, te im je koeficijent sličnosti
slični, te im je koeficijent sličnosti 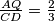 . Kao i u drugom koraku, uočavamo da je zbroj visina ta
. Kao i u drugom koraku, uočavamo da je zbroj visina ta  trokuta
trokuta  , stoga je visina trokuta
, stoga je visina trokuta 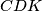 iz vrha
iz vrha  jednaka
jednaka 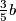 .
.
5. korak: Računanje 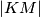
Kao i u 3. koraku, uočavamo sličnost trokuta 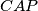 i
i 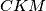 zbog paralelnosti
zbog paralelnosti 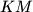 i
i  . Koeficijent sličnosti im je jednak omjeru visina. Kako
. Koeficijent sličnosti im je jednak omjeru visina. Kako 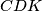 i
i 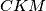 imaju jednaku visinu, koeficijent sličnosti im je
imaju jednaku visinu, koeficijent sličnosti im je  .
.
Dakle 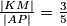 , pa jer je
, pa jer je 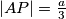 , zaključujemo
, zaključujemo 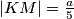 .
.
6. korak: Računanje površine
Sada znamo duljine 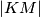 i
i 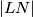 , pa lako računamo površinu
, pa lako računamo površinu 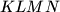 kao
kao 
Zaključujemo da je omjer površina 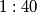
Kao rješenje upišite 140
Često je u zadacima s površinom, pogotovo u onima u kojima se pojavljuju četverokuti, korisno razmišljati o Talesovom poučku i omjerima.
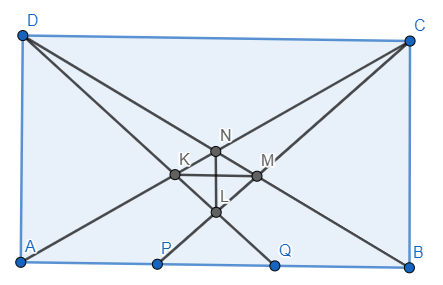
\textbf{Zadatak:} Točke $P$ i $Q$ leže na stranici $AB$ pravokutnika $ABCD$ tako da vrijedi $|AP| = |PQ| = |QB|$. Pravac $DQ$ siječe pravce $AC$ i $CP$ redom u točkama $K$ i $L$, a pravac $DB$ siječe pravce $AC$ i $CP$ redom u točkama $N$ i $M$.
Odredite omjer površina četverokuta $KLMN$ i pravokutnika $ABCD$.
\textbf{Rješenje:}
\\
\includegraphics{01a.png}
\\
\textbf{1. korak: Formula za površinu $KLMN$} \\ Primijetimo da zbog simetrije vrijedi $KM || AB$ i $LN || BC$, stoga su dijagonale četverokuta $KLMN$ okomite. To znači da je površina četverokuta $KLMN = \frac{KM\cdot LN}2$. Sada nam cilj postaje odrediti omjer $KM$ i $AB$, te $LN$ i $BC$. Označimo $a = |AB|$ i $b=|BC|$.
\textbf{2. korak: Računanje visine trokuta $PQL$} \\
Za početak, primijetimo da su trokuti $PQL$ i $DCL$ slični, te da im je koeficijent sličnosti $1:3$ (jer je $|DC| = 3|PQ|$). To znači da je visina trokuta $PQL$ jednaka trećini visine $DCL$. Jasno je da je zbroj te $2$ visine $BC$, stoga je $v_{PQ} = \frac{|BC|}4$.
\textbf{3. korak: Računanje $|NL|$} \\
Lako je vidjeti da su trokuti $ABN$ i $DCN$ sukladni, te da im je zbroj visina jednak $BC$ - zato su im visine $\frac{|BC|}2$. Zbog paralelnosti $NL$ i $BC$, dužinu $|NL|$ možemo prikazati kao razliku duljina visina $ABN$ i $PQL$.
Zbog toga, $|NL| = \frac{|BC|}4$.
\textbf{4. korak: Računanje visine trokuta $CDK$}
\\
Primijetimo tako da su trokuti $CDK$ i $AQK$ slični, te im je koeficijent sličnosti $\frac{AQ}{CD} = \frac 23$. Kao i u drugom koraku, uočavamo da je zbroj visina ta $2$ trokuta $BC$, stoga je visina trokuta $CDK$ iz vrha $K$ jednaka $\frac 35 b$.
\textbf{5. korak: Računanje $|KM|$}
\\
Kao i u 3. koraku, uočavamo sličnost trokuta $CAP$ i $CKM$ zbog paralelnosti $KM$ i $AB$. Koeficijent sličnosti im je jednak omjeru visina. Kako $CDK$ i $CKM$ imaju jednaku visinu, koeficijent sličnosti im je $\frac 35$.
Dakle $\frac {|KM|}{|AP|} = \frac 35$, pa jer je $|AP| = \frac a3$, zaključujemo $|KM| = \frac a5$.
\textbf{6. korak: Računanje površine}
\\
Sada znamo duljine $|KM|$ i $|LN|$, pa lako računamo površinu $KLMN$ kao
$$\frac 12 |KM|\cdot |LN| = \frac 12 \cdot \frac 35 b \cdot \frac a5 = \frac 1{40} ab$$
Zaključujemo da je omjer površina $1:40$
\\\\
Kao rješenje upišite 140
 i
i  leže na stranici
leže na stranici  pravokutnika
pravokutnika  tako da vrijedi
tako da vrijedi 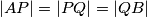 . Pravac
. Pravac 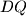 siječe pravce
siječe pravce  i
i 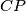 redom u točkama
redom u točkama  i
i  , a pravac
, a pravac 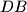 siječe pravce
siječe pravce  i
i 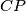 redom u točkama
redom u točkama  i
i  . Odredite omjer površina četverokuta
. Odredite omjer površina četverokuta 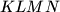 i pravokutnika
i pravokutnika  .
.
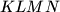
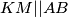 i
i 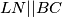 , stoga su dijagonale četverokuta
, stoga su dijagonale četverokuta 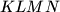 okomite. To znači da je površina četverokuta
okomite. To znači da je površina četverokuta 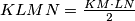 . Sada nam cilj postaje odrediti omjer
. Sada nam cilj postaje odrediti omjer 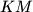 i
i  , te
, te 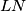 i
i  . Označimo
. Označimo 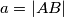 i
i 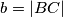 .
.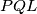
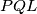 i
i 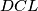 slični, te da im je koeficijent sličnosti
slični, te da im je koeficijent sličnosti 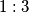 (jer je
(jer je 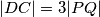 ). To znači da je visina trokuta
). To znači da je visina trokuta 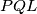 jednaka trećini visine
jednaka trećini visine 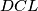 . Jasno je da je zbroj te
. Jasno je da je zbroj te  visine
visine  , stoga je
, stoga je 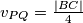 .
.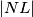
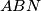 i
i 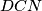 sukladni, te da im je zbroj visina jednak
sukladni, te da im je zbroj visina jednak  - zato su im visine
- zato su im visine 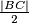 . Zbog paralelnosti
. Zbog paralelnosti 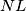 i
i  , dužinu
, dužinu 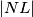 možemo prikazati kao razliku duljina visina
možemo prikazati kao razliku duljina visina 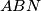 i
i 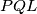 .
.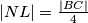 .
.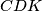
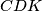 i
i 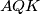 slični, te im je koeficijent sličnosti
slični, te im je koeficijent sličnosti 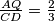 . Kao i u drugom koraku, uočavamo da je zbroj visina ta
. Kao i u drugom koraku, uočavamo da je zbroj visina ta  trokuta
trokuta  , stoga je visina trokuta
, stoga je visina trokuta 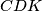 iz vrha
iz vrha  jednaka
jednaka 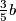 .
.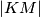
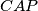 i
i 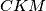 zbog paralelnosti
zbog paralelnosti 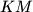 i
i  . Koeficijent sličnosti im je jednak omjeru visina. Kako
. Koeficijent sličnosti im je jednak omjeru visina. Kako 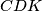 i
i 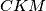 imaju jednaku visinu, koeficijent sličnosti im je
imaju jednaku visinu, koeficijent sličnosti im je  .
.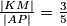 , pa jer je
, pa jer je 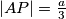 , zaključujemo
, zaključujemo 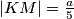 .
.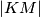 i
i 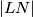 , pa lako računamo površinu
, pa lako računamo površinu 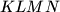 kao
kao