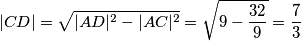Promotrimo još jedan zadatak gdje nam je korisno primijeniti Pitagorin poučak da bismo mogli izjednačiti 2 formule za površinu trokuta.
Zadatak: Dana je dužina  duljine
duljine  . Neka su
. Neka su  i
i  (
(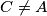 ) točke na kružnici s promjerom
) točke na kružnici s promjerom  takve da vrijedi
takve da vrijedi 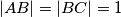 . Izračunaj
. Izračunaj 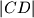 .
.
Rješenje:
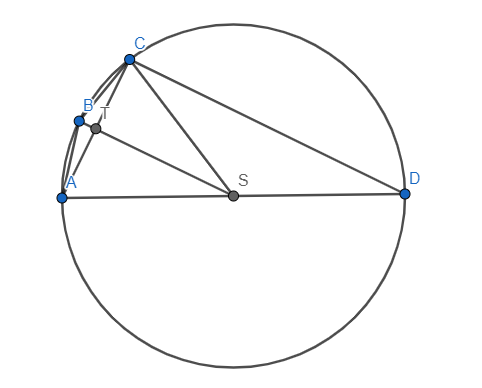
1. korak: Uočimo pravokutni trokut
Zbog Talesovog poučka o obodnom kutu nad promjerom kružnice, vrijedi da je kut 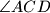 pravi. Zato je
pravi. Zato je  pravokutan, pa ćemo
pravokutan, pa ćemo  izračunati korištenjem Pitagorinog poučka:
izračunati korištenjem Pitagorinog poučka: 
2 korak: Poveznica  i
i 
Sad želimo saznati koliki je  . Kako imamo točku
. Kako imamo točku  koju još nismo iskoristili, a znamo da je
koju još nismo iskoristili, a znamo da je 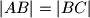 , slutimo da bi ih nekako trebalo povezati. Zato označimo sa
, slutimo da bi ih nekako trebalo povezati. Zato označimo sa  središte kružnice, te s
središte kružnice, te s  označavamo sjecište
označavamo sjecište  i
i  .
.
Promotrimo sada trokute 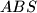 i
i 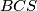 . Kako znamo da su
. Kako znamo da su 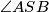 i
i 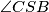 jednaki, lako (iz jednakokračnih trokuta kojima su krakovi radijusi kružnice) vidimo da su i
jednaki, lako (iz jednakokračnih trokuta kojima su krakovi radijusi kružnice) vidimo da su i 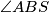 i
i 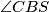 jednaki. Sada po poučku
jednaki. Sada po poučku 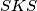 o sukladnosti dobijemo da su trokuti
o sukladnosti dobijemo da su trokuti 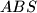 i
i 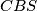 sukladni pa zaključujemo da je
sukladni pa zaključujemo da je  , a iz toga
, a iz toga 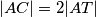 .
.
3 korak: Računamo površinu ABS
|AT| je visina jednakokračnog trokuta 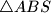 na krak. Kako tom trokutu znamo sve stranice (radijusi
na krak. Kako tom trokutu znamo sve stranice (radijusi  ,
, 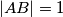 ), izračunajmo mu površinu.
), izračunajmo mu površinu.
Kako je jednakokračan, lako mu dobijamo visinu na osnovicu koristeći Pitagorin poučak na pravokutni trokut čije su stranice jedan krak, pola osnovice i visina.
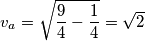
Sada lako dobijamo da je površina trokuta 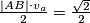
4 korak: Računamo AT
Sada jednostavno prikažemo površinu 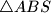 kao pola umnoška kraka i visine na krak.
kao pola umnoška kraka i visine na krak.
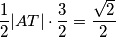
Sada jednostavno vidimo da je 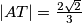 .
.
5 korak: Računamo CD
Zaključujemo da je 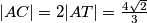 .
.
Uvrštavanjem u Pitagorin poučak, 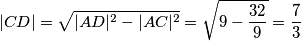
Kao rješenje upišite "Tales"
Promotrimo još jedan zadatak gdje nam je korisno primijeniti Pitagorin poučak da bismo mogli izjednačiti 2 formule za površinu trokuta.
\textbf{Zadatak:} Dana je dužina $AD$ duljine $3$. Neka su $B$ i $C$ ($C \neq A$) točke na kružnici s promjerom $AD$ takve da vrijedi $|AB| = |BC| = 1$. Izračunaj $|CD|$.
\textbf{Rješenje:}
\\
\includegraphics{000a.png}
\\
\textbf{1. korak: Uočimo pravokutni trokut} \\ Zbog Talesovog poučka o obodnom kutu nad promjerom kružnice, vrijedi da je kut $\angle ACD$ pravi. Zato je $ACD$ pravokutan, pa ćemo $CD$ izračunati korištenjem \textbf{Pitagorinog poučka}:
$$|CD| = \sqrt{|AD|^2 - |AC|^2} = \sqrt{9- |AC|^2}$$
\textbf{2 korak: Poveznica $AC$ i $B$} \\ Sad želimo saznati koliki je $AC$. Kako imamo točku $B$ koju još nismo iskoristili, a znamo da je $|AB| = |BC|$, slutimo da bi ih nekako trebalo povezati. Zato označimo sa $S$ središte kružnice, te s $T$ označavamo sjecište $AC$ i $BS$.
Promotrimo sada trokute $ABS$ i $BCS$. Kako znamo da su $\angle ASB$ i $\angle CSB$ jednaki, lako (iz jednakokračnih trokuta kojima su krakovi radijusi kružnice) vidimo da su i $\angle ABS$ i $\angle CBS$ jednaki. Sada po poučku $SKS$ o sukladnosti dobijemo da su trokuti $ABS$ i $CBS$ sukladni pa zaključujemo da je $|AT| = |TC|$, a iz toga $|AC| = 2 |AT|$.
\textbf{3 korak: Računamo površinu ABS} \\ |AT| je visina jednakokračnog trokuta $\triangle ABS$ na krak. Kako tom trokutu znamo sve stranice (radijusi $\frac 32$ , $|AB| = 1$), izračunajmo mu površinu.
Kako je jednakokračan, lako mu dobijamo visinu na osnovicu koristeći Pitagorin poučak na pravokutni trokut čije su stranice jedan krak, pola osnovice i visina.
$$v_a = \sqrt{\frac 94 - \frac 14} = \sqrt 2$$
Sada lako dobijamo da je površina trokuta $\frac {|AB| \cdot v_a}2 = \frac{\sqrt{2}}2$
\textbf{4 korak: Računamo AT} \\Sada jednostavno prikažemo površinu $\triangle ABS$ kao pola umnoška kraka i visine na krak.
$$\frac 12 |AT|\cdot \frac 32 = \frac {\sqrt 2}2$$
Sada jednostavno vidimo da je $|AT| = \frac{2\sqrt 2}3$.
\textbf{5 korak: Računamo CD} \\ Zaključujemo da je $|AC|= 2|AT|= \frac {4\sqrt 2}3$.
Uvrštavanjem u Pitagorin poučak,
$$|CD| = \sqrt{|AD|^2 - |AC|^2} = \sqrt{9- \frac{32}9} = \frac 73$$
\\
\\
Kao rješenje upišite "Tales"
 duljine
duljine  . Neka su
. Neka su  i
i  (
(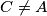 ) točke na kružnici s promjerom
) točke na kružnici s promjerom  takve da vrijedi
takve da vrijedi 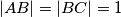 . Izračunaj
. Izračunaj 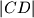 .
.
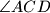 pravi. Zato je
pravi. Zato je  pravokutan, pa ćemo
pravokutan, pa ćemo  izračunati korištenjem Pitagorinog poučka:
izračunati korištenjem Pitagorinog poučka: 
 i
i 
 . Kako imamo točku
. Kako imamo točku  koju još nismo iskoristili, a znamo da je
koju još nismo iskoristili, a znamo da je 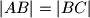 , slutimo da bi ih nekako trebalo povezati. Zato označimo sa
, slutimo da bi ih nekako trebalo povezati. Zato označimo sa  središte kružnice, te s
središte kružnice, te s  označavamo sjecište
označavamo sjecište  i
i  .
.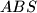 i
i 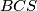 . Kako znamo da su
. Kako znamo da su 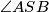 i
i 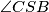 jednaki, lako (iz jednakokračnih trokuta kojima su krakovi radijusi kružnice) vidimo da su i
jednaki, lako (iz jednakokračnih trokuta kojima su krakovi radijusi kružnice) vidimo da su i 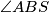 i
i 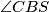 jednaki. Sada po poučku
jednaki. Sada po poučku 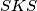 o sukladnosti dobijemo da su trokuti
o sukladnosti dobijemo da su trokuti 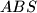 i
i 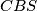 sukladni pa zaključujemo da je
sukladni pa zaključujemo da je  , a iz toga
, a iz toga 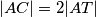 .
.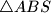 na krak. Kako tom trokutu znamo sve stranice (radijusi
na krak. Kako tom trokutu znamo sve stranice (radijusi  ,
, 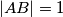 ), izračunajmo mu površinu.
), izračunajmo mu površinu.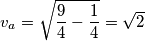
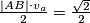
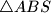 kao pola umnoška kraka i visine na krak.
kao pola umnoška kraka i visine na krak.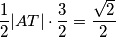
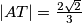 .
.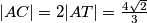 .
.