Dobrodošli u novi tjedan MetaMatha gdje ćemo obrađivati Invarijante i monovarijante!
U mnogim logičko-kombinatornim zadacima znanje pronalaska invarijante ili monovarijante igra ključnu ulogu u rješavanju problema. Ukoliko imamo u zadatku neki proces (igru, niz poteza, transformacija) invarijantna vrijednost je ona vrijednost (veličina, promatrana pojava) koja se ne mijenja odabirom dozvoljenih poteza u problemu. Monovarijanta je vrijednost koja opada ili raste (ili ne raste ili ne opada). Sljedeći primjeri demonstrirati će kako riješiti zadatak koristeći invarijante/monovarijante, te dati potrebnu intuiciju za samostalnim pronalaskom istih u narednim zadacima. Primjeri su odabrani tako da pokrivaju više razina težina zadataka, kako bi vam pokazali lakše a i teže probleme koje možete očekivati zadacima za samostalni rad.
Primjer 1:
Na ploči je napisano  brojeva. U svakom koraku radimo sljedeću transformaciju: odabiremo bilo koja tri broja
brojeva. U svakom koraku radimo sljedeću transformaciju: odabiremo bilo koja tri broja  i zamijenimo ih brojevima
i zamijenimo ih brojevima  . Ukoliko su na početku napisani brojevi
. Ukoliko su na početku napisani brojevi 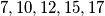 možemo li uzastopnim ponavljanjem opisanog postupka doći do brojeva
možemo li uzastopnim ponavljanjem opisanog postupka doći do brojeva 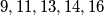 ?
?
Rješenje:
Zadatak prikazuje neki niz događaja (transformacija, poteza) što nas odmah može motivirati da bar probamo problem riješiti pronalaskom neke invarijante. U svakom koraku zamjenjujemo  s
s  . Primijetimo da je
. Primijetimo da je 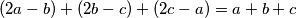 , što nam sugerira da navedenom zamjenom brojeva njihova suma ostaje ista. Stoga, kao invarijantnu vrijednost svakog koraka gledamo sumu svih brojeva na ploči. Ona ne ovisi o odabiru brojeva koje zamjenjujemo svakim korakom, ostaje ista nakon svake transformacije.
, što nam sugerira da navedenom zamjenom brojeva njihova suma ostaje ista. Stoga, kao invarijantnu vrijednost svakog koraka gledamo sumu svih brojeva na ploči. Ona ne ovisi o odabiru brojeva koje zamjenjujemo svakim korakom, ostaje ista nakon svake transformacije.
Konkretno, pošto je suma svih brojeva na ploči uvijek nepromijenjena, te na početku iznosi 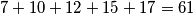 , nemoguće je dobiti brojeve na ploči čija će suma biti
, nemoguće je dobiti brojeve na ploči čija će suma biti 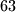 (
(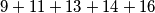 ).
).
Kako biste dobili  bod za ovaj primjer unesite broj
bod za ovaj primjer unesite broj  kao rješenje zadatka.
kao rješenje zadatka.
Dobrodošli u novi tjedan MetaMatha gdje ćemo obrađivati \textbf{Invarijante i monovarijante}!
U mnogim logičko-kombinatornim zadacima znanje pronalaska invarijante ili monovarijante igra ključnu ulogu u rješavanju problema. Ukoliko imamo u zadatku neki proces (igru, niz poteza, transformacija) invarijantna vrijednost je ona vrijednost (veličina, promatrana pojava) koja se ne mijenja odabirom dozvoljenih poteza u problemu. Monovarijanta je vrijednost koja opada ili raste (ili ne raste ili ne opada). Sljedeći primjeri demonstrirati će kako riješiti zadatak koristeći invarijante/monovarijante, te dati potrebnu intuiciju za samostalnim pronalaskom istih u narednim zadacima. Primjeri su odabrani tako da pokrivaju više razina težina zadataka, kako bi vam pokazali lakše a i teže probleme koje možete očekivati zadacima za samostalni rad.
\textbf{Primjer 1:}
Na ploči je napisano $5$ brojeva. U svakom koraku radimo sljedeću transformaciju: odabiremo bilo koja tri broja $a,b,c$ i zamijenimo ih brojevima $2a-b, 2b-c, 2c-a$. Ukoliko su na početku napisani brojevi $7,10,12,15,17$ možemo li uzastopnim ponavljanjem opisanog postupka doći do brojeva $9,11,13,14,16$ ?
\textbf{Rješenje:}
Zadatak prikazuje neki niz događaja (transformacija, poteza) što nas odmah može motivirati da bar probamo problem riješiti pronalaskom neke invarijante. U svakom koraku zamjenjujemo $a,b,c$ s $2a-b, 2b-c, 2c-a$. Primijetimo da je $(2a-b)+(2b-c)+(2c-a)=a+b+c$, što nam sugerira da navedenom zamjenom brojeva njihova suma ostaje ista. Stoga, kao invarijantnu vrijednost svakog koraka gledamo sumu svih brojeva na ploči. Ona ne ovisi o odabiru brojeva koje zamjenjujemo svakim korakom, ostaje ista nakon svake transformacije.
Konkretno, pošto je suma svih brojeva na ploči uvijek nepromijenjena, te na početku iznosi $7+10+12+15+17=61$, nemoguće je dobiti brojeve na ploči čija će suma biti $63$ ($9+11+13+14+16$).
Kako biste dobili $1$ bod za ovaj primjer unesite broj $1$ kao rješenje zadatka.
 brojeva. U svakom koraku radimo sljedeću transformaciju: odabiremo bilo koja tri broja
brojeva. U svakom koraku radimo sljedeću transformaciju: odabiremo bilo koja tri broja  i zamijenimo ih brojevima
i zamijenimo ih brojevima  . Ukoliko su na početku napisani brojevi
. Ukoliko su na početku napisani brojevi 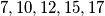 možemo li uzastopnim ponavljanjem opisanog postupka doći do brojeva
možemo li uzastopnim ponavljanjem opisanog postupka doći do brojeva 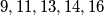 ?
? s
s  . Primijetimo da je
. Primijetimo da je 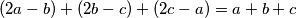 , što nam sugerira da navedenom zamjenom brojeva njihova suma ostaje ista. Stoga, kao invarijantnu vrijednost svakog koraka gledamo sumu svih brojeva na ploči. Ona ne ovisi o odabiru brojeva koje zamjenjujemo svakim korakom, ostaje ista nakon svake transformacije.
, što nam sugerira da navedenom zamjenom brojeva njihova suma ostaje ista. Stoga, kao invarijantnu vrijednost svakog koraka gledamo sumu svih brojeva na ploči. Ona ne ovisi o odabiru brojeva koje zamjenjujemo svakim korakom, ostaje ista nakon svake transformacije.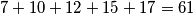 , nemoguće je dobiti brojeve na ploči čija će suma biti
, nemoguće je dobiti brojeve na ploči čija će suma biti 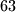 (
(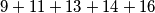 ).
). bod za ovaj primjer unesite broj
bod za ovaj primjer unesite broj  kao rješenje zadatka.
kao rješenje zadatka. 