Invarijante i monovarijante - Primjer 2
Primjer 2:
Na otoku se nalazi  crvenih kameleona,
crvenih kameleona, 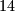 plavih i
plavih i 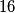 zelenih. Kada se sretnu dva kameleona različitih boja, oba promijene boju u onu treću. Može li se dogoditi da svi kameleoni postanu iste boje?
zelenih. Kada se sretnu dva kameleona različitih boja, oba promijene boju u onu treću. Može li se dogoditi da svi kameleoni postanu iste boje?
Rješenje:
U ovom zadatku invarijanta je već malo suptilnija nego u prethodnom primjeru. Najbolji način za početi zadatak je simulirati nekoliko koraka i probati uočiti neku pravilnost u broju crvenih, plavih i zelenih kameleona. U svakom koraku kad se susretnu dva kameleona različitih boja, broj kameleona tih boja se smanji za  dok se broj kameleona treće boje poveća za
dok se broj kameleona treće boje poveća za  . Tražimo nešto što je isto kad mu oduzmemo
. Tražimo nešto što je isto kad mu oduzmemo  ili mu dodamo
ili mu dodamo  . To nas dovodi do promatranja ostataka broja kameleona pri dijeljenju s brojem
. To nas dovodi do promatranja ostataka broja kameleona pri dijeljenju s brojem  .
.
Kako se prilikom svakog sudara broj kameleona pojedine boje ili poveća za  ili smanji za
ili smanji za  , zaključujemo da se u svakom susretu ostatak pri dijeljenju broja pripadnika svake vrste s 3 promijeni, i to tako da se poveća točno za dva. Na početku su svi ostatci broja kameleona pojedine vrste pri dijeljenju s
, zaključujemo da se u svakom susretu ostatak pri dijeljenju broja pripadnika svake vrste s 3 promijeni, i to tako da se poveća točno za dva. Na početku su svi ostatci broja kameleona pojedine vrste pri dijeljenju s  međusobno različiti, te će stoga takvi i ostati nakon svakog poteza. Kada bi mogli postići da svi kameleoni budu iste boje, ostaci broja svih vrsta pri dijeljenju s
međusobno različiti, te će stoga takvi i ostati nakon svakog poteza. Kada bi mogli postići da svi kameleoni budu iste boje, ostaci broja svih vrsta pri dijeljenju s  bi bili jednaki
bi bili jednaki  , što je nemoguće.
, što je nemoguće.
Za dobivanje  boda za ovaj primjer unesite broj
boda za ovaj primjer unesite broj  kao rješenje zadatka.
kao rješenje zadatka.
