Primjer 3:
Vrhovi pravilnog  -terokuta označeni su realnim brojevima
-terokuta označeni su realnim brojevima 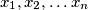 . Neka su
. Neka su 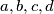 proizvoljne četiri uzastopne oznake. Ako je
proizvoljne četiri uzastopne oznake. Ako je 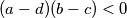 , možemo zamijeniti
, možemo zamijeniti  i
i  . Možemo li provoditi zamijene brojeva na opisani način proizvoljno mnogo puta?
. Možemo li provoditi zamijene brojeva na opisani način proizvoljno mnogo puta?
Rješenje:
Ovaj zadatak je primjer kako pronaći monovarijantu koja nam daje odgovor na pitanje iz zadatka. Ideja je opet slična, promatrati neku vrijednost za koju možemo nešto zaključiti (ili ostaje ista ili raste/pada) nakon svakog koraka.
Ako je 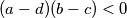 , to znači da je
, to znači da je 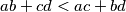 . Tada možemo zamijeniti brojeve
. Tada možemo zamijeniti brojeve  i
i  . Na što nas to može motivirati? Imamo izraz
. Na što nas to može motivirati? Imamo izraz  , što na neki način predstavlja zbroj umnožaka susjednih brojeva (nedostaje
, što na neki način predstavlja zbroj umnožaka susjednih brojeva (nedostaje 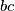 ). Nakon zamjene mjesta
). Nakon zamjene mjesta  i
i  , izraz
, izraz 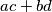 opet predstavlja zbroj umnožaka susjednih brojeva (opet bez
opet predstavlja zbroj umnožaka susjednih brojeva (opet bez 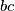 ).
).
Motivirani time, promotrimo zbroj umnožaka svih brojeva na ploči: 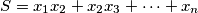 . Za odabrane susjedne
. Za odabrane susjedne 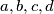 , možemo
, možemo  zapisati kao
zapisati kao  , gdje
, gdje  predstavlja preostali dio sume. Ako je
predstavlja preostali dio sume. Ako je 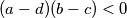 , tj.
, tj. 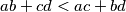 , zamjenjujemo
, zamjenjujemo  i
i  . Time smo dobili novu sumu svih uzastopnih parova:
. Time smo dobili novu sumu svih uzastopnih parova: 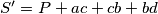 , gdje
, gdje  ostaje nepromijenjen jer transformacija ne utječe na njega. Iz ovoga direktno slijedi da je
ostaje nepromijenjen jer transformacija ne utječe na njega. Iz ovoga direktno slijedi da je 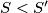 (jer je
(jer je 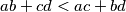 ), što znači da je suma umnožaka parova uzastopnih brojeva strogo rastuća prilikom svake transformacije.
), što znači da je suma umnožaka parova uzastopnih brojeva strogo rastuća prilikom svake transformacije.
Možemo li provoditi zamjene brojeva proizvoljno mnogo puta? Primijetimo da mogućih vrijednosti broja  ima konačno mnogo. Za dane
ima konačno mnogo. Za dane 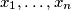 postoji konačno mnogo rasporeda kako ih pridružiti vrhovima danog
postoji konačno mnogo rasporeda kako ih pridružiti vrhovima danog  -terokuta, te kako svaki raspored daje jednu vrijednost
-terokuta, te kako svaki raspored daje jednu vrijednost  , postoji konačno mnogo vrijednosti koje može poprimiti broj
, postoji konačno mnogo vrijednosti koje može poprimiti broj  . Ovakav argument je dovoljan za ovaj zadatak, no možemo biti još precizniji pa reći da sigurno nema više od
. Ovakav argument je dovoljan za ovaj zadatak, no možemo biti još precizniji pa reći da sigurno nema više od 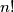 vrijednosti za
vrijednosti za  pošto postoji toliko različitih permutacija danih brojeva
pošto postoji toliko različitih permutacija danih brojeva 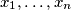 . Na linku možete pronaći dodatne materijale ako želite saznati više o prebrojavanjima.
. Na linku možete pronaći dodatne materijale ako želite saznati više o prebrojavanjima.
Kako svaka transformacija strogo poveća vrijednost broja  kojih ima konačno mnogo, zaključujemo da ne možemo proizvoljno mnogo puta provesti opisanu zamjenu iz zadatka.
kojih ima konačno mnogo, zaključujemo da ne možemo proizvoljno mnogo puta provesti opisanu zamjenu iz zadatka.
Za dobivanje  boda za ovaj primjer unesite broj
boda za ovaj primjer unesite broj  kao rješenje zadatka. Sretno u rješavanju idućih lanaca!
kao rješenje zadatka. Sretno u rješavanju idućih lanaca!
\textbf{Primjer 3:}
Vrhovi pravilnog $n$-terokuta označeni su realnim brojevima $x_1,x_2,\dotsc x_n$. Neka su $a,b,c,d$ proizvoljne četiri uzastopne oznake. Ako je $(a-d)(b-c)<0$, možemo zamijeniti $b$ i $c$. Možemo li provoditi zamijene brojeva na opisani način proizvoljno mnogo puta?
\textbf{Rješenje:}
Ovaj zadatak je primjer kako pronaći monovarijantu koja nam daje odgovor na pitanje iz zadatka. Ideja je opet slična, promatrati neku vrijednost za koju možemo nešto zaključiti (ili ostaje ista ili raste/pada) nakon svakog koraka.
Ako je $(a-d)(b-c)<0$, to znači da je $ab+cd<ac+bd$. Tada možemo zamijeniti brojeve $b$ i $c$. Na što nas to može motivirati? Imamo izraz $ab+cd$, što na neki način predstavlja zbroj umnožaka susjednih brojeva (nedostaje $bc$). Nakon zamjene mjesta $b$ i $c$, izraz $ac+bd$ opet predstavlja zbroj umnožaka susjednih brojeva (opet bez $bc$).
Motivirani time, promotrimo zbroj umnožaka svih brojeva na ploči: $S=x_1x_2 + x_2x_3 +\cdots +x_n$. Za odabrane susjedne $a,b,c,d$, možemo $S$ zapisati kao $S=P+ab+bc+cd$, gdje $P$ predstavlja preostali dio sume. Ako je $(a-d)(b-c)<0$, tj. $ab+cd<ac+bd$, zamjenjujemo $b$ i $c$. Time smo dobili novu sumu svih uzastopnih parova: $S'=P+ac+cb+bd$, gdje $P$ ostaje nepromijenjen jer transformacija ne utječe na njega. Iz ovoga direktno slijedi da je $S<S'$ (jer je $ab+cd<ac+bd$), što znači da je suma umnožaka parova uzastopnih brojeva strogo rastuća prilikom svake transformacije.
Možemo li provoditi zamjene brojeva proizvoljno mnogo puta? Primijetimo da mogućih vrijednosti broja $S$ ima konačno mnogo. Za dane $x_1,\dotsc,x_n$ postoji konačno mnogo rasporeda kako ih pridružiti vrhovima danog $n$-terokuta, te kako svaki raspored daje jednu vrijednost $S$, postoji konačno mnogo vrijednosti koje može poprimiti broj $S$.
Ovakav argument je dovoljan za ovaj zadatak, no možemo biti još precizniji pa reći da sigurno nema više od $n!$ vrijednosti za $S$ pošto postoji toliko različitih permutacija danih brojeva $x_1,\dotsc ,x_n$. Na \href{https://www.skoljka.org/media/attachment/2/00245_wbptr8zbdph3287p75xr/predavanja_2020_2021__L8.pdf}{linku} možete pronaći dodatne materijale ako želite saznati više o prebrojavanjima.
Kako svaka transformacija strogo poveća vrijednost broja $S$ kojih ima konačno mnogo, zaključujemo da ne možemo proizvoljno mnogo puta provesti opisanu zamjenu iz zadatka.
Za dobivanje $1$ boda za ovaj primjer unesite broj $3$ kao rješenje zadatka. Sretno u rješavanju idućih lanaca!
 -terokuta označeni su realnim brojevima
-terokuta označeni su realnim brojevima 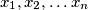 . Neka su
. Neka su 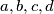 proizvoljne četiri uzastopne oznake. Ako je
proizvoljne četiri uzastopne oznake. Ako je 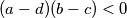 , možemo zamijeniti
, možemo zamijeniti  i
i  . Možemo li provoditi zamijene brojeva na opisani način proizvoljno mnogo puta?
. Možemo li provoditi zamijene brojeva na opisani način proizvoljno mnogo puta?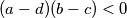 , to znači da je
, to znači da je 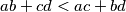 . Tada možemo zamijeniti brojeve
. Tada možemo zamijeniti brojeve  i
i  . Na što nas to može motivirati? Imamo izraz
. Na što nas to može motivirati? Imamo izraz  , što na neki način predstavlja zbroj umnožaka susjednih brojeva (nedostaje
, što na neki način predstavlja zbroj umnožaka susjednih brojeva (nedostaje 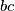 ). Nakon zamjene mjesta
). Nakon zamjene mjesta  i
i  , izraz
, izraz 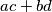 opet predstavlja zbroj umnožaka susjednih brojeva (opet bez
opet predstavlja zbroj umnožaka susjednih brojeva (opet bez 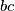 ).
).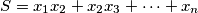 . Za odabrane susjedne
. Za odabrane susjedne 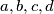 , možemo
, možemo  zapisati kao
zapisati kao  , gdje
, gdje  predstavlja preostali dio sume. Ako je
predstavlja preostali dio sume. Ako je 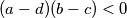 , tj.
, tj. 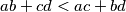 , zamjenjujemo
, zamjenjujemo  i
i  . Time smo dobili novu sumu svih uzastopnih parova:
. Time smo dobili novu sumu svih uzastopnih parova: 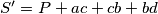 , gdje
, gdje  ostaje nepromijenjen jer transformacija ne utječe na njega. Iz ovoga direktno slijedi da je
ostaje nepromijenjen jer transformacija ne utječe na njega. Iz ovoga direktno slijedi da je 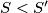 (jer je
(jer je 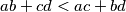 ), što znači da je suma umnožaka parova uzastopnih brojeva strogo rastuća prilikom svake transformacije.
), što znači da je suma umnožaka parova uzastopnih brojeva strogo rastuća prilikom svake transformacije. ima konačno mnogo. Za dane
ima konačno mnogo. Za dane 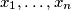 postoji konačno mnogo rasporeda kako ih pridružiti vrhovima danog
postoji konačno mnogo rasporeda kako ih pridružiti vrhovima danog  -terokuta, te kako svaki raspored daje jednu vrijednost
-terokuta, te kako svaki raspored daje jednu vrijednost  , postoji konačno mnogo vrijednosti koje može poprimiti broj
, postoji konačno mnogo vrijednosti koje može poprimiti broj  . Ovakav argument je dovoljan za ovaj zadatak, no možemo biti još precizniji pa reći da sigurno nema više od
. Ovakav argument je dovoljan za ovaj zadatak, no možemo biti još precizniji pa reći da sigurno nema više od 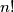 vrijednosti za
vrijednosti za  pošto postoji toliko različitih permutacija danih brojeva
pošto postoji toliko različitih permutacija danih brojeva 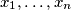 . Na linku možete pronaći dodatne materijale ako želite saznati više o prebrojavanjima.
. Na linku možete pronaći dodatne materijale ako želite saznati više o prebrojavanjima. kojih ima konačno mnogo, zaključujemo da ne možemo proizvoljno mnogo puta provesti opisanu zamjenu iz zadatka.
kojih ima konačno mnogo, zaključujemo da ne možemo proizvoljno mnogo puta provesti opisanu zamjenu iz zadatka. boda za ovaj primjer unesite broj
boda za ovaj primjer unesite broj  kao rješenje zadatka. Sretno u rješavanju idućih lanaca!
kao rješenje zadatka. Sretno u rješavanju idućih lanaca! 