Zadatak 2:
Ploča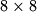 
obojana je crno-bijelo kao standardna šahovska ploča. U pojedinom potezu treba odabrati jedan redak ili stupac i svakom od 
polja u tom retku promijeniti boju iz crne u bijeli i obrnuto. Može li se konačnim nizom takvih poteza postići da točno jedno polje na ploči bude crno?
\textbf{Zadatak 2:}
Ploča $8\times 8$ obojana je crno-bijelo kao standardna šahovska ploča. U pojedinom potezu treba odabrati jedan redak ili stupac i svakom od $8$ polja u tom retku promijeniti boju iz crne u bijeli i obrnuto. Može li se konačnim nizom takvih poteza postići da točno jedno polje na ploči bude crno?
