MetaMath '23

\textbf{Primjer 1.} U skupu realnih brojeva riješite jednadžbu 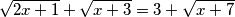\[\sqrt{2x+1}+\sqrt{x+3}=3+\sqrt{x+7}\] \textbf{Rješenje.} Ovo je jedna od mnogih vrsti jednadžbi s kojima ćete se susresti na natjecanjima, i kao i sve ostale, ima neke trikove. Mogli bismo ovakvu zadanu odmah kvadrirati i mučiti se s faktorizacijama i korijenima, ali mogli bismo malo bolje ju namjestit. Primjetimo da kada kvadriramo, slobodni koeficijenti koje ćemo imati su 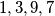$1,3,9,7$ a koeficijenti uz $x$ će biti $2,1,0,1$. 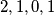Pa vidi ti to! Možemo namjestiti jednadžbu da nam se svi pokrate kad kvadriramo. 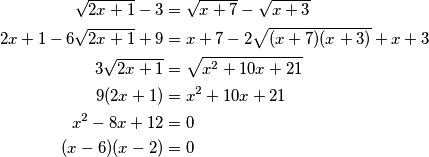\begin{align*} \sqrt{2x+1}-3&=\sqrt{x+7}-\sqrt{x+3}\\ 2x+1-6\sqrt{2x+1}+9&=x+7-2\sqrt{(x+7)(x+3)}+x+3\\ 3\sqrt{2x+1}&=\sqrt{x^2+10x+21}\\ 9(2x+1)&=x^2+10x+21\\ x^2-8x+12&=0\\ (x-6)(x-2)&=0 \end{align*} Sada preostaje samo provjeriti ova rješenja jer smo kvadriranjem mogli dobiti neko rješenje viška te vidimo da za 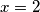$x=2$ ne vrijedi jednakost dok za 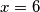$x=6$ vrijedi pa je jedino rješenje 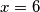$x=6$. Kako biste dobili bod upišite 1 kao rješenje.