Primjer 2. Gargamel je uhvatio  Štrumfova i raspodijelio ih u tri vreće. Kad je Papu Štrumfa iz prve vreće premjestio u drugu, Mrguda iz druge u treću, a Štrumfetu iz treće u prvu, prosječna visina Štrumfova u prvoj vreći se smanjila za
Štrumfova i raspodijelio ih u tri vreće. Kad je Papu Štrumfa iz prve vreće premjestio u drugu, Mrguda iz druge u treću, a Štrumfetu iz treće u prvu, prosječna visina Štrumfova u prvoj vreći se smanjila za  milimetara, a prosječne visine Štrumfova u drugoj i trećoj vreći su se povećale redom za
milimetara, a prosječne visine Štrumfova u drugoj i trećoj vreći su se povećale redom za  milimetara i
milimetara i  milimetara. Ako je u prvoj vreći bilo devet Štrumfova, odredite
milimetara. Ako je u prvoj vreći bilo devet Štrumfova, odredite  .
.
Rješenje. Za početak ćemo se baviti linearnim sustavom jednadžbi, tj. postavljanju takvog sustava iz nekog teksta. Za početak, neka je u drugoj vreći bilo  , a u trećoj vreći
, a u trećoj vreći  Štrumfova. Analizirajmo zadatak dio po dio i slažimo jednadžbe.
Štrumfova. Analizirajmo zadatak dio po dio i slažimo jednadžbe.
Neka je  visina Pape Štrumfa,
visina Pape Štrumfa,  visina Mrguda i
visina Mrguda i  visina Štrumfete. Kako je iz svake vreće premjestio nekog u drugu broj po vrećama je ostao isti, samo se prosječna visina promjenila. Neka su
visina Štrumfete. Kako je iz svake vreće premjestio nekog u drugu broj po vrećama je ostao isti, samo se prosječna visina promjenila. Neka su 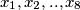 visine Štrumfova koji su ostali u prvoj vreći, tada je njihova prosječna visina na početku bila
visine Štrumfova koji su ostali u prvoj vreći, tada je njihova prosječna visina na početku bila 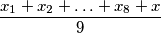 , a nakon promjene
, a nakon promjene 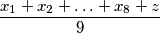 te znamo da je druga prosječna visina smanjila za
te znamo da je druga prosječna visina smanjila za  , tj. u obliku jednadžbe to je
, tj. u obliku jednadžbe to je 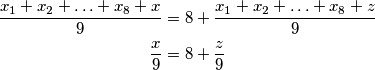 Isto tako postavljamo jednadžbe za prosjek u drugim dvjema vrećama i dobivamo
Isto tako postavljamo jednadžbe za prosjek u drugim dvjema vrećama i dobivamo 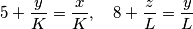 Sada imamo sustav
Sada imamo sustav 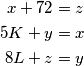 Zbrajanjem sve 3 jednadžbe nam se pokrate
Zbrajanjem sve 3 jednadžbe nam se pokrate 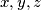 te imamo
te imamo 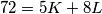 što je diofantska jednadžba za
što je diofantska jednadžba za 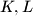 . Vidimo da
. Vidimo da  dijeli
dijeli 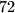 , a i
, a i 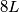 pa treba dijeliti i
pa treba dijeliti i 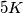 što znači da je
što znači da je  višekratnik broja
višekratnik broja  . Ako imamo
. Ako imamo 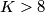 tada je
tada je 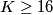 pa imamo da je
pa imamo da je 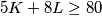 , a zbroj treba biti 72 pa je taj slučaj nemoguć. Dakle, nužno vrijedi
, a zbroj treba biti 72 pa je taj slučaj nemoguć. Dakle, nužno vrijedi 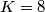 i iz toga dobijemo
i iz toga dobijemo 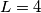 pa je
pa je 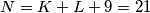 .
.
Kako biste dobili bod na ovom zadatku, upišite 2 kao rješenje.
\textbf{Primjer 2.} Gargamel je uhvatio $N$ Štrumfova i raspodijelio ih u tri vreće. Kad je Papu Štrumfa iz prve vreće premjestio u drugu, Mrguda iz druge u treću, a Štrumfetu iz treće u prvu, prosječna visina Štrumfova u prvoj vreći se smanjila za $8$ milimetara, a prosječne visine Štrumfova u drugoj i trećoj vreći su se povećale redom za $5$ milimetara i $8$ milimetara. Ako je u prvoj vreći bilo devet Štrumfova, odredite $N$.
\textbf{Rješenje.} Za početak ćemo se baviti linearnim sustavom jednadžbi, tj. postavljanju takvog sustava iz nekog teksta. Za početak, neka je u drugoj vreći bilo $K$, a u trećoj vreći $L$ Štrumfova. Analizirajmo zadatak dio po dio i slažimo jednadžbe.
Neka je $x$ visina Pape Štrumfa, $y$ visina Mrguda i $z$ visina Štrumfete. Kako je iz svake vreće premjestio nekog u drugu broj po vrećama je ostao isti, samo se prosječna visina promjenila. Neka su $x_1,x_2,..,x_8$ visine Štrumfova koji su ostali u prvoj vreći, tada je njihova prosječna visina na početku bila $\dfrac{x_1+x_2+\ldots+x_8+x}{9}$, a nakon promjene $\dfrac{x_1+x_2+\ldots+x_8+z}{9}$ te znamo da je druga prosječna visina smanjila za $8$, tj. u obliku jednadžbe to je
\begin{align*}
\dfrac{x_1+x_2+\ldots+x_8+x}{9}&=8+\dfrac{x_1+x_2+\ldots+x_8+z}{9}\\
\frac{x}{9}&=8+\frac{z}{9}
\end{align*}
Isto tako postavljamo jednadžbe za prosjek u drugim dvjema vrećama i dobivamo
\[5+\frac{y}{K}=\frac{x}{K},\quad8+\frac{z}{L}=\frac{y}{L}\]
Sada imamo sustav
\begin{align*}
x+72&=z\\
5K+y&=x\\
8L+z&=y
\end{align*}
Zbrajanjem sve 3 jednadžbe nam se pokrate $x,y,z$ te imamo $72=5K+8L$ što je diofantska jednadžba za $K,L$. Vidimo da $8$ dijeli $72$, a i $8L$ pa treba dijeliti i $5K$ što znači da je $K$ višekratnik broja $8$. Ako imamo $K>8$ tada je $K\geq16$ pa imamo da je $5K+8L\geq80$, a zbroj treba biti 72 pa je taj slučaj nemoguć. Dakle, nužno vrijedi $K=8$ i iz toga dobijemo $L=4$ pa je $N=K+L+9=21$.
Kako biste dobili bod na ovom zadatku, upišite 2 kao rješenje.
 Štrumfova i raspodijelio ih u tri vreće. Kad je Papu Štrumfa iz prve vreće premjestio u drugu, Mrguda iz druge u treću, a Štrumfetu iz treće u prvu, prosječna visina Štrumfova u prvoj vreći se smanjila za
Štrumfova i raspodijelio ih u tri vreće. Kad je Papu Štrumfa iz prve vreće premjestio u drugu, Mrguda iz druge u treću, a Štrumfetu iz treće u prvu, prosječna visina Štrumfova u prvoj vreći se smanjila za  milimetara, a prosječne visine Štrumfova u drugoj i trećoj vreći su se povećale redom za
milimetara, a prosječne visine Štrumfova u drugoj i trećoj vreći su se povećale redom za  milimetara i
milimetara i  milimetara. Ako je u prvoj vreći bilo devet Štrumfova, odredite
milimetara. Ako je u prvoj vreći bilo devet Štrumfova, odredite  .
. , a u trećoj vreći
, a u trećoj vreći  Štrumfova. Analizirajmo zadatak dio po dio i slažimo jednadžbe.
Štrumfova. Analizirajmo zadatak dio po dio i slažimo jednadžbe. visina Pape Štrumfa,
visina Pape Štrumfa,  visina Mrguda i
visina Mrguda i  visina Štrumfete. Kako je iz svake vreće premjestio nekog u drugu broj po vrećama je ostao isti, samo se prosječna visina promjenila. Neka su
visina Štrumfete. Kako je iz svake vreće premjestio nekog u drugu broj po vrećama je ostao isti, samo se prosječna visina promjenila. Neka su 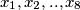 visine Štrumfova koji su ostali u prvoj vreći, tada je njihova prosječna visina na početku bila
visine Štrumfova koji su ostali u prvoj vreći, tada je njihova prosječna visina na početku bila 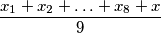 , a nakon promjene
, a nakon promjene 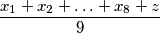 te znamo da je druga prosječna visina smanjila za
te znamo da je druga prosječna visina smanjila za  , tj. u obliku jednadžbe to je
, tj. u obliku jednadžbe to je 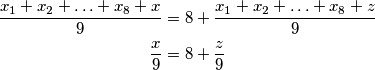 Isto tako postavljamo jednadžbe za prosjek u drugim dvjema vrećama i dobivamo
Isto tako postavljamo jednadžbe za prosjek u drugim dvjema vrećama i dobivamo 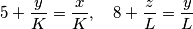 Sada imamo sustav
Sada imamo sustav 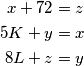 Zbrajanjem sve 3 jednadžbe nam se pokrate
Zbrajanjem sve 3 jednadžbe nam se pokrate 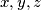 te imamo
te imamo 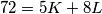 što je diofantska jednadžba za
što je diofantska jednadžba za 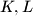 . Vidimo da
. Vidimo da  dijeli
dijeli 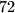 , a i
, a i 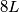 pa treba dijeliti i
pa treba dijeliti i 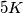 što znači da je
što znači da je  višekratnik broja
višekratnik broja  . Ako imamo
. Ako imamo 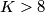 tada je
tada je 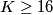 pa imamo da je
pa imamo da je 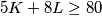 , a zbroj treba biti 72 pa je taj slučaj nemoguć. Dakle, nužno vrijedi
, a zbroj treba biti 72 pa je taj slučaj nemoguć. Dakle, nužno vrijedi 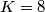 i iz toga dobijemo
i iz toga dobijemo 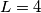 pa je
pa je 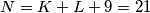 .
.