Primjer 3. Nađite sva realna rješenja jednadžbe 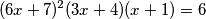
Rješenje. U ovom dijelu primjera posvetiti ćemo se kvadratnim jednadžbama i trikovima uz njih. Možda ćete primjetiti da je zadana jednadžba četvrtog stupnja, ali to ne znači da nam kvadratna ne može pomoći. Za početak bismo mogli samo bezumno ovo razmonžiti i pogađati rješenja te se nadati da se ovo faktorizira. To je jako puno posla, i na mnogo mjesta nam se može dogoditi računska pogreška. Također, moguće je da ovo nema racionalih rješenje pa nam pogađanje ne bi nimalo pomoglo, ali srećom postoji dosta lakši i brži način.
Za početak pomnožimo jednadžbu s 3. Ovo nije nužno ali nam pomaže uočiti nešto. 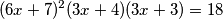 Sada imamo jednadžbu oblika
Sada imamo jednadžbu oblika 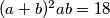 . Ovo je i dalje jednadžba četvrtog stupnja, a njih ne znamo uvijek riješiti. No, što ako namjestimo da ipak izgleda kao kvadratna, za to bi trebali nekako "maknuti" linearni i kubni član. Tu dolazimo do trika koji nam razlika kvadrata motivira. Želimo "pomaknuti"
. Ovo je i dalje jednadžba četvrtog stupnja, a njih ne znamo uvijek riješiti. No, što ako namjestimo da ipak izgleda kao kvadratna, za to bi trebali nekako "maknuti" linearni i kubni član. Tu dolazimo do trika koji nam razlika kvadrata motivira. Želimo "pomaknuti"  za neku vrijednost da na izrazima
za neku vrijednost da na izrazima 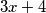 i
i 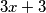 možemo primjeniti razliku kvadrata, tj.
možemo primjeniti razliku kvadrata, tj. 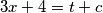 ,
, 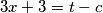 . Zbrajanjem i oduzimanjem ovih jednadžbi dobivamo
. Zbrajanjem i oduzimanjem ovih jednadžbi dobivamo 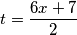 i
i 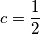 . Pa uvrstimo to i dobivamo
. Pa uvrstimo to i dobivamo 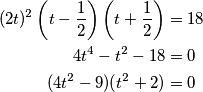 Sada kako je
Sada kako je 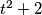 uvijek pozitivno dobivamo da je
uvijek pozitivno dobivamo da je 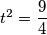 , odnosno da je
, odnosno da je 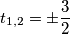 . Uvrštavanjem natrag u
. Uvrštavanjem natrag u 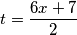 dobijemo da su rješenja jednadžbe
dobijemo da su rješenja jednadžbe 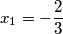 i
i 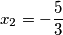 .
.
Kako biste dobili bod na ovom zadatku upišite 3 kao rješenje.
\textbf{Primjer 3.} Nađite sva realna rješenja jednadžbe \[(6x+7)^2(3x+4)(x+1)=6\]
\textbf{Rješenje.} U ovom dijelu primjera posvetiti ćemo se kvadratnim jednadžbama i trikovima uz njih. Možda ćete primjetiti da je zadana jednadžba četvrtog stupnja, ali to ne znači da nam kvadratna ne može pomoći. Za početak bismo mogli samo bezumno ovo razmonžiti i pogađati rješenja te se nadati da se ovo faktorizira. To je jako puno posla, i na mnogo mjesta nam se može dogoditi računska pogreška. Također, moguće je da ovo nema racionalih rješenje pa nam pogađanje ne bi nimalo pomoglo, ali srećom postoji dosta lakši i brži način.
Za početak pomnožimo jednadžbu s 3. Ovo nije nužno ali nam pomaže uočiti nešto.
\[(6x+7)^2(3x+4)(3x+3)=18\]
Sada imamo jednadžbu oblika $(a+b)^2ab=18$. Ovo je i dalje jednadžba četvrtog stupnja, a njih ne znamo uvijek riješiti. No, što ako namjestimo da ipak izgleda kao kvadratna, za to bi trebali nekako "maknuti" linearni i kubni član. Tu dolazimo do trika koji nam razlika kvadrata motivira. Želimo "pomaknuti" $x$ za neku vrijednost da na izrazima $3x+4$ i $3x+3$ možemo primjeniti razliku kvadrata, tj. $3x+4=t+c$, $3x+3=t-c$. Zbrajanjem i oduzimanjem ovih jednadžbi dobivamo $t=\dfrac{6x+7}{2}$ i $c=\dfrac{1}{2}$. Pa uvrstimo to i dobivamo
\begin{align*}
(2t)^2\left(t-\frac{1}{2}\right)\left(t+\frac{1}{2}\right)&=18\\
4t^4-t^2-18&=0\\
(4t^2-9)(t^2+2)&=0
\end{align*}
Sada kako je $t^2+2$ uvijek pozitivno dobivamo da je $t^2=\dfrac{9}{4}$, odnosno da je $t_{1,2}=\pm\dfrac{3}{2}$. Uvrštavanjem natrag u $t=\dfrac{6x+7}{2}$ dobijemo da su rješenja jednadžbe $x_1=-\dfrac{2}{3}$ i $x_2=-\dfrac{5}{3}$.
Kako biste dobili bod na ovom zadatku upišite 3 kao rješenje.
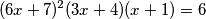
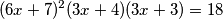 Sada imamo jednadžbu oblika
Sada imamo jednadžbu oblika 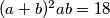 . Ovo je i dalje jednadžba četvrtog stupnja, a njih ne znamo uvijek riješiti. No, što ako namjestimo da ipak izgleda kao kvadratna, za to bi trebali nekako "maknuti" linearni i kubni član. Tu dolazimo do trika koji nam razlika kvadrata motivira. Želimo "pomaknuti"
. Ovo je i dalje jednadžba četvrtog stupnja, a njih ne znamo uvijek riješiti. No, što ako namjestimo da ipak izgleda kao kvadratna, za to bi trebali nekako "maknuti" linearni i kubni član. Tu dolazimo do trika koji nam razlika kvadrata motivira. Želimo "pomaknuti"  za neku vrijednost da na izrazima
za neku vrijednost da na izrazima 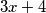 i
i 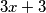 možemo primjeniti razliku kvadrata, tj.
možemo primjeniti razliku kvadrata, tj. 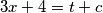 ,
, 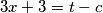 . Zbrajanjem i oduzimanjem ovih jednadžbi dobivamo
. Zbrajanjem i oduzimanjem ovih jednadžbi dobivamo 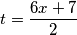 i
i 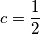 . Pa uvrstimo to i dobivamo
. Pa uvrstimo to i dobivamo 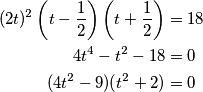 Sada kako je
Sada kako je 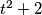 uvijek pozitivno dobivamo da je
uvijek pozitivno dobivamo da je 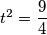 , odnosno da je
, odnosno da je 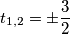 . Uvrštavanjem natrag u
. Uvrštavanjem natrag u 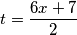 dobijemo da su rješenja jednadžbe
dobijemo da su rješenja jednadžbe 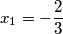 i
i 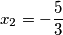 .
.