Primjer 4. Nađite sve uređene parove realnih brojeva 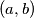 koji su rješenja sustava
koji su rješenja sustava 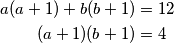
Rješenje Kao i u prošlom zadatku, ovdje ćemo se poslužiti trikom. Kada raspišemo ove izraze imamo 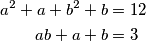 U ovom obliku ne možemo puno toga napraviti, izraziti
U ovom obliku ne možemo puno toga napraviti, izraziti  preko
preko  će nas samo dovest do nekih ludih razlomaka i visokih potencija, ali u jednadžbi nam se pojavljuje zbroj i umnožak brojeva
će nas samo dovest do nekih ludih razlomaka i visokih potencija, ali u jednadžbi nam se pojavljuje zbroj i umnožak brojeva  i
i  , a zbroj kvadrata se lako izrazi preko njih. Pa, što ako mi ovo pokušamo riješiti za
, a zbroj kvadrata se lako izrazi preko njih. Pa, što ako mi ovo pokušamo riješiti za  i
i 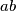 ? Druga jednadžba će nam postati linearna a prva će biti kvadratna, s tim možemo vrlo lako raditi. I tako, stavimo
? Druga jednadžba će nam postati linearna a prva će biti kvadratna, s tim možemo vrlo lako raditi. I tako, stavimo 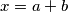 ,
, 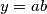 te iz toga i dobijemo
te iz toga i dobijemo 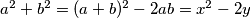 . Sada imamo
. Sada imamo
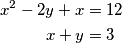 Sada možemo pomnožiti 2. jednadžbu s 2 i dodati ju prvoj te imamo
Sada možemo pomnožiti 2. jednadžbu s 2 i dodati ju prvoj te imamo 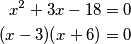 Sada za
Sada za 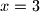 imamo
imamo 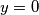 odnosno
odnosno 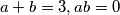 pa su rješenje
pa su rješenje 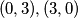 te za
te za 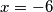 imamo
imamo 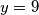 . Sada primjetimo da ako su
. Sada primjetimo da ako su 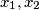 nultočke kvadratne, tj.
nultočke kvadratne, tj. 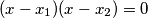 tada raspisivanjem imamo
tada raspisivanjem imamo 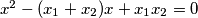 , pa kako imamo što je
, pa kako imamo što je  i
i 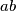 možemo to odmah uvrstiti u kvadratnu kojoj će rješenja biti
možemo to odmah uvrstiti u kvadratnu kojoj će rješenja biti 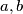
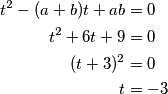 Dakle, rješenje kvadratne, a i ujedno vrijednosti od
Dakle, rješenje kvadratne, a i ujedno vrijednosti od 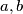 su
su 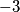 pa su sve uređene trojke
pa su sve uređene trojke 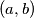 tada
tada 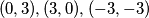 .
.
Kako biste dobili bod na ovom zadatku kao rješenje upišite 4.
\textbf{Primjer 4.} Nađite sve uređene parove realnih brojeva $(a,b)$ koji su rješenja sustava
\begin{align*}
a(a+1)+b(b+1)&=12\\
(a+1)(b+1)&=4
\end{align*}
\textbf{Rješenje} Kao i u prošlom zadatku, ovdje ćemo se poslužiti trikom. Kada raspišemo ove izraze imamo
\begin{align*}
a^2+a+b^2+b&=12\\
ab+a+b&=3
\end{align*}
U ovom obliku ne možemo puno toga napraviti, izraziti $a$ preko $b$ će nas samo dovest do nekih ludih razlomaka i visokih potencija, ali u jednadžbi nam se pojavljuje zbroj i umnožak brojeva $a$ i $b$, a zbroj kvadrata se lako izrazi preko njih. Pa, što ako mi ovo pokušamo riješiti za $a+b$ i $ab$? Druga jednadžba će nam postati linearna a prva će biti kvadratna, s tim možemo vrlo lako raditi.
I tako, stavimo $x=a+b$, $y=ab$ te iz toga i dobijemo $a^2+b^2=(a+b)^2-2ab=x^2-2y$. Sada imamo
\begin{align*}
x^2-2y+x&=12\\
x+y&=3
\end{align*}
Sada možemo pomnožiti 2. jednadžbu s 2 i dodati ju prvoj te imamo
\begin{align*}
x^2+3x-18&=0\\
(x-3)(x+6)&=0
\end{align*}
Sada za $x=3$ imamo $y=0$ odnosno $a+b=3, ab=0$ pa su rješenje $(0,3),(3,0)$ te za $x=-6$ imamo $y=9$. Sada primjetimo da ako su $x_1,x_2$ nultočke kvadratne, tj. $(x-x_1)(x-x_2)=0$ tada raspisivanjem imamo $x^2-(x_1+x_2)x+x_1x_2=0$, pa kako imamo što je $a+b$ i $ab$ možemo to odmah uvrstiti u kvadratnu kojoj će rješenja biti $a,b$
\begin{align*}
t^2-(a+b)t+ab&=0\\
t^2+6t+9&=0\\
(t+3)^2&=0\\
t&=-3
\end{align*}
Dakle, rješenje kvadratne, a i ujedno vrijednosti od $a,b$ su $-3$ pa su sve uređene trojke $(a,b)$ tada $(0,3),(3,0),(-3,-3)$.
Kako biste dobili bod na ovom zadatku kao rješenje upišite 4.
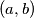 koji su rješenja sustava
koji su rješenja sustava 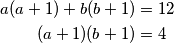
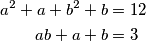 U ovom obliku ne možemo puno toga napraviti, izraziti
U ovom obliku ne možemo puno toga napraviti, izraziti  preko
preko  će nas samo dovest do nekih ludih razlomaka i visokih potencija, ali u jednadžbi nam se pojavljuje zbroj i umnožak brojeva
će nas samo dovest do nekih ludih razlomaka i visokih potencija, ali u jednadžbi nam se pojavljuje zbroj i umnožak brojeva  i
i  , a zbroj kvadrata se lako izrazi preko njih. Pa, što ako mi ovo pokušamo riješiti za
, a zbroj kvadrata se lako izrazi preko njih. Pa, što ako mi ovo pokušamo riješiti za  i
i 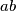 ? Druga jednadžba će nam postati linearna a prva će biti kvadratna, s tim možemo vrlo lako raditi. I tako, stavimo
? Druga jednadžba će nam postati linearna a prva će biti kvadratna, s tim možemo vrlo lako raditi. I tako, stavimo 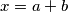 ,
, 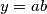 te iz toga i dobijemo
te iz toga i dobijemo 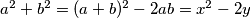 . Sada imamo
. Sada imamo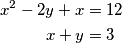 Sada možemo pomnožiti 2. jednadžbu s 2 i dodati ju prvoj te imamo
Sada možemo pomnožiti 2. jednadžbu s 2 i dodati ju prvoj te imamo 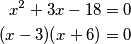 Sada za
Sada za 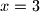 imamo
imamo 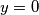 odnosno
odnosno 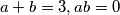 pa su rješenje
pa su rješenje 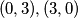 te za
te za 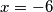 imamo
imamo 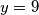 . Sada primjetimo da ako su
. Sada primjetimo da ako su 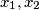 nultočke kvadratne, tj.
nultočke kvadratne, tj. 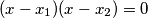 tada raspisivanjem imamo
tada raspisivanjem imamo 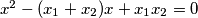 , pa kako imamo što je
, pa kako imamo što je  i
i 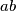 možemo to odmah uvrstiti u kvadratnu kojoj će rješenja biti
možemo to odmah uvrstiti u kvadratnu kojoj će rješenja biti 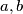
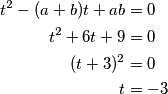 Dakle, rješenje kvadratne, a i ujedno vrijednosti od
Dakle, rješenje kvadratne, a i ujedno vrijednosti od 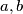 su
su 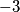 pa su sve uređene trojke
pa su sve uređene trojke 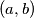 tada
tada 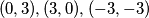 .
.