Zadatak 3.
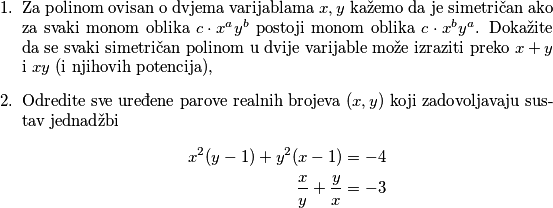
\textbf{Zadatak 3.}
\begin{enumerate}
\item Za polinom ovisan o dvjema varijablama $x,y$ kažemo da je simetričan ako za svaki monom oblika $c\cdot x^ay^b$ postoji monom oblika $c\cdot x^by^a$. Dokažite da se svaki simetričan polinom u dvije varijable može izraziti preko $x+y$ i $xy$ (i njihovih potencija),
\item Odredite sve uređene parove realnih brojeva $(x,y)$ koji zadovoljavaju sustav jednadžbi
\begin{align*}
x^2(y-1)+y^2(x-1)&=-4\\
\dfrac{x}{y}+\dfrac{y}{x}&=-3
\end{align*}
\end{enumerate}