Promatrati ostatke koje članovi u jednadžbi daju prilikom dijeljenja nekim brojem  često kažemo kraće kao promatrati jednadžbu modulo
često kažemo kraće kao promatrati jednadžbu modulo  .
.
Do sada smo možda najčešće gledali jednadžbe modulo  (parnost izraza u jednadžbi) ili modulo
(parnost izraza u jednadžbi) ili modulo  (zadnja znamenka izraza), no možemo birati i druge module. Dapače, češće ćemo moći nešto više zaključiti gledajući modulo neki drugi
(zadnja znamenka izraza), no možemo birati i druge module. Dapače, češće ćemo moći nešto više zaključiti gledajući modulo neki drugi  .
.
Kako izabrati  ?
? 
Vratimo se na potpune kvadrate. Naime, promatrajući potpune kvadrate i njihove ostatke modulo  ,
,  i
i  , možemo zaključiti:
, možemo zaključiti:  Dokažimo tvrdnju za modulo
Dokažimo tvrdnju za modulo  , pozivamo vas da vi dokažete preostale tvrdnje. To možemo napraviti koristeći kongruencije, koristeći mali Fermatov teorem, ili koristeći zapis
, pozivamo vas da vi dokažete preostale tvrdnje. To možemo napraviti koristeći kongruencije, koristeći mali Fermatov teorem, ili koristeći zapis 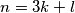 , gdje je
, gdje je 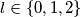 mogući ostatak koji
mogući ostatak koji  daje pri dijeljenju s
daje pri dijeljenju s  .
.
Svaki broj  zapisiv je kao
zapisiv je kao 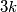 ,
, 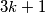 ili
ili 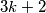 , ovisno o ostatku modulo
, ovisno o ostatku modulo  . Kvadrati tih brojeva su
. Kvadrati tih brojeva su 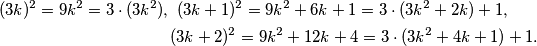 Odavde zaista vidimo da svaka mogućnost vodi na ostatak
Odavde zaista vidimo da svaka mogućnost vodi na ostatak  ili
ili  modulo
modulo  .
.
Prije nastavka, osvrnimo se i na potpune kubove: 
Pogledajmo jedan primjer kako ovo iskoristiti.
Primjer.
Odredi rješenja jednadžbe 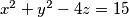 u cijelim brojevima.
u cijelim brojevima.
Rješenje.
Budući da nam se javljaju potpuni kvadrati, možemo gledati ostatke modulo  ,
,  ili
ili  . Nadalje, kako imamo član
. Nadalje, kako imamo član 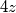 , nema smisla gledati jednadžbu modulo
, nema smisla gledati jednadžbu modulo  , budući da čak ako članovi ostatci brojeva
, budući da čak ako članovi ostatci brojeva  i
i 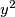 imaju reducirani skup mogućnosti, broj
imaju reducirani skup mogućnosti, broj 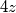 može davati bilo koji ostatak modulo
može davati bilo koji ostatak modulo  .
.
Zato pogledajmo jednadžbu modulo  . Desna strana daje ostatak
. Desna strana daje ostatak  . Član
. Član 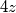 uvijek je djeljiv s
uvijek je djeljiv s  . Na kraju, svaki od kvadrata
. Na kraju, svaki od kvadrata  ,
, 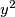 može davati ostatak nula ili jedan, pa njihova suma može davati ostatke
može davati ostatak nula ili jedan, pa njihova suma može davati ostatke 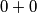 ,
, 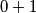 ,
, 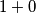 ili
ili 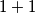 .
.
Kada sve to zajedno spojimo, lijeva strana može davati ostatke  ,
,  ili
ili  pri dijeljenju s
pri dijeljenju s  , dok desna daje ostatak
, dok desna daje ostatak  , neovisno o odabiru cijelih brojeva
, neovisno o odabiru cijelih brojeva  ,
,  i
i  . Odavde zaključujemo da jednadžba nema rješenja u cijelim brojevima.
. Odavde zaključujemo da jednadžba nema rješenja u cijelim brojevima.
Da smo odabrali neki drugi  i gledali jednadžbu modulo taj
i gledali jednadžbu modulo taj  , no dobili da postoji slučaj u kojem lijeva i desna strana daju isti ostatak, sigurno ne bismo mogli zaključiti da jednadžba zato ima ili nema rješenja. No, tada bismo možda mogli zaključiti nešto drugo.
, no dobili da postoji slučaj u kojem lijeva i desna strana daju isti ostatak, sigurno ne bismo mogli zaključiti da jednadžba zato ima ili nema rješenja. No, tada bismo možda mogli zaključiti nešto drugo.
Upišite 1 za nastavak.
Promatrati ostatke koje članovi u jednadžbi daju prilikom dijeljenja nekim brojem $N$ često kažemo kraće kao \textit{promatrati jednadžbu modulo $N$}.
Do sada smo možda najčešće gledali jednadžbe modulo $2$ (parnost izraza u jednadžbi) ili modulo $10$ (zadnja znamenka izraza), no možemo birati i druge module. Dapače, češće ćemo moći nešto više zaključiti gledajući modulo neki drugi $N$.
Kako izabrati $N$?
\begin{itemize}
\item Brojevi koji se već pojavljuju u jednadžbama -- ako već imamo neki broj u jednadžbi, ili ako vidimo da će nekoliko sumanada zbog tog broja biti djeljivo neki brojem $N$, to za preostale članove u jednadžbi znači da imamo manje slučajeva za gledati ako gledamo jednadžbu modulo $N$.
\item Ako u jednadžbi imamo izraze oblika $2^a$, $3^b$, ... -- u tim slučajevima, može biti korisno jednadžbu modulo $2$ ili $3$ redom, u vidu prošle natuknice, a možemo gledati i modulo $4$ ili $8$, te $9$ redom, nadajući se da ćemo moći zaključiti da za $a$ veće od $2$ ili $3$, odnosno za $b$ veće od $2$ jednadžba nema rješenja.
\item Ako u jednadžbi imamo potpun kvadrat -- u tim slučajevima korisni su moduli $3$, $4$ i $8$, vidjet ćemo kasnije zašto.
\item Ako u jednadžbi imamo potpun kub -- u tim slučajevima može biti korisno gledati jednadžbu modulo $7$.
\item Ako nemamo druge ideje, onda redom $2,3,4,5,7,8,9,\ldots$ (nema smisla gledati modulo $6$ i $10$ ako smo gledali modulo $2$ i $3$, odnosno $2$ i $5$).
\end{itemize}
Vratimo se na potpune kvadrate. Naime, promatrajući potpune kvadrate i njihove ostatke modulo $3$, $4$ i $8$, možemo zaključiti:
\begin{itemize}
\item potpuni kvadrati daju ostatak $0$ ili $1$ modulo $3$;
\item potpuni kvadrati daju ostatak $0$ ili $1$ modulo $4$;
\item potpuni kvadrati daju ostatak $0$, $1$ ili $4$ modulo $8$.
\end{itemize}
Dokažimo tvrdnju za modulo $3$, pozivamo vas da vi dokažete preostale tvrdnje. To možemo napraviti koristeći kongruencije, koristeći mali Fermatov teorem, ili koristeći zapis $n = 3k+l$, gdje je $l \in \{ 0,1,2 \}$ mogući ostatak koji $n$ daje pri dijeljenju s $3$.
Svaki broj $n$ zapisiv je kao $3k$, $3k+1$ ili $3k+2$, ovisno o ostatku modulo $3$. Kvadrati tih brojeva su
\begin{multline*}
(3k)^2 = 9k^2 = 3 \cdot (3k^2), \ (3k+1)^2 = 9k^2 + 6k +1 = 3 \cdot (3k^2 + 2k) + 1, \\
(3k+2)^2 = 9k^2 + 12k +4 = 3 \cdot (3k^2 + 4k + 1) + 1 .
\end{multline*}
Odavde zaista vidimo da svaka mogućnost vodi na ostatak $0$ ili $1$ modulo $3$.
Prije nastavka, osvrnimo se i na potpune kubove:
\begin{itemize}
\item potpuni kubovi daju ostatak $0$, $1$ ili $6$ modulo $7$.
\end{itemize}
Pogledajmo jedan primjer kako ovo iskoristiti.
\textbf{Primjer.}
Odredi rješenja jednadžbe $x^2 + y^2 - 4z = 15$ u cijelim brojevima.
\textbf{Rješenje.}
Budući da nam se javljaju potpuni kvadrati, možemo gledati ostatke modulo $3$, $4$ ili $8$. Nadalje, kako imamo član $4z$, nema smisla gledati jednadžbu modulo $3$, budući da čak ako članovi ostatci brojeva $x^2$ i $y^2$ imaju reducirani skup mogućnosti, broj $4z$ može davati bilo koji ostatak modulo $3$.
Zato pogledajmo jednadžbu modulo $4$. Desna strana daje ostatak $3$. Član $4z$ uvijek je djeljiv s $4$. Na kraju, svaki od kvadrata $x^2$, $y^2$ može davati ostatak nula ili jedan, pa njihova suma može davati ostatke $0+0$, $0+1$, $1+0$ ili $1+1$.
Kada sve to zajedno spojimo, lijeva strana može davati ostatke $0$, $1$ ili $2$ pri dijeljenju s $4$, dok desna daje ostatak $3$, neovisno o odabiru cijelih brojeva $x$, $y$ i $z$. Odavde zaključujemo da jednadžba nema rješenja u cijelim brojevima.
Da smo odabrali neki drugi $N$ i gledali jednadžbu modulo taj $N$, no dobili da postoji slučaj u kojem lijeva i desna strana daju isti ostatak, sigurno ne bismo mogli zaključiti da jednadžba zato ima ili nema rješenja. No, tada bismo možda mogli zaključiti nešto drugo.
Upišite 1 za nastavak.
 često kažemo kraće kao promatrati jednadžbu modulo
često kažemo kraće kao promatrati jednadžbu modulo  .
. (parnost izraza u jednadžbi) ili modulo
(parnost izraza u jednadžbi) ili modulo  (zadnja znamenka izraza), no možemo birati i druge module. Dapače, češće ćemo moći nešto više zaključiti gledajući modulo neki drugi
(zadnja znamenka izraza), no možemo birati i druge module. Dapače, češće ćemo moći nešto više zaključiti gledajući modulo neki drugi  .
. ?
? 
 ,
,  i
i  , možemo zaključiti:
, možemo zaključiti:  Dokažimo tvrdnju za modulo
Dokažimo tvrdnju za modulo  , pozivamo vas da vi dokažete preostale tvrdnje. To možemo napraviti koristeći kongruencije, koristeći mali Fermatov teorem, ili koristeći zapis
, pozivamo vas da vi dokažete preostale tvrdnje. To možemo napraviti koristeći kongruencije, koristeći mali Fermatov teorem, ili koristeći zapis 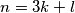 , gdje je
, gdje je 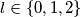 mogući ostatak koji
mogući ostatak koji  daje pri dijeljenju s
daje pri dijeljenju s  .
. zapisiv je kao
zapisiv je kao 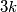 ,
, 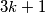 ili
ili 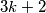 , ovisno o ostatku modulo
, ovisno o ostatku modulo  . Kvadrati tih brojeva su
. Kvadrati tih brojeva su 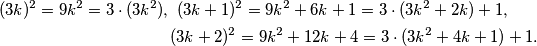 Odavde zaista vidimo da svaka mogućnost vodi na ostatak
Odavde zaista vidimo da svaka mogućnost vodi na ostatak  ili
ili  modulo
modulo  .
.
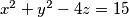 u cijelim brojevima.
u cijelim brojevima. ,
,  ili
ili  . Nadalje, kako imamo član
. Nadalje, kako imamo član 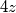 , nema smisla gledati jednadžbu modulo
, nema smisla gledati jednadžbu modulo  , budući da čak ako članovi ostatci brojeva
, budući da čak ako članovi ostatci brojeva  i
i 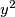 imaju reducirani skup mogućnosti, broj
imaju reducirani skup mogućnosti, broj 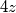 može davati bilo koji ostatak modulo
može davati bilo koji ostatak modulo  .
. . Desna strana daje ostatak
. Desna strana daje ostatak  . Član
. Član 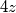 uvijek je djeljiv s
uvijek je djeljiv s  . Na kraju, svaki od kvadrata
. Na kraju, svaki od kvadrata  ,
, 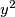 može davati ostatak nula ili jedan, pa njihova suma može davati ostatke
može davati ostatak nula ili jedan, pa njihova suma može davati ostatke 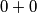 ,
, 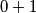 ,
, 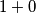 ili
ili 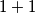 .
. ,
,  ili
ili  pri dijeljenju s
pri dijeljenju s  , dok desna daje ostatak
, dok desna daje ostatak  , neovisno o odabiru cijelih brojeva
, neovisno o odabiru cijelih brojeva  ,
,  i
i  . Odavde zaključujemo da jednadžba nema rješenja u cijelim brojevima.
. Odavde zaključujemo da jednadžba nema rješenja u cijelim brojevima. i gledali jednadžbu modulo taj
i gledali jednadžbu modulo taj  , no dobili da postoji slučaj u kojem lijeva i desna strana daju isti ostatak, sigurno ne bismo mogli zaključiti da jednadžba zato ima ili nema rješenja. No, tada bismo možda mogli zaključiti nešto drugo.
, no dobili da postoji slučaj u kojem lijeva i desna strana daju isti ostatak, sigurno ne bismo mogli zaključiti da jednadžba zato ima ili nema rješenja. No, tada bismo možda mogli zaključiti nešto drugo.