Kao što smo najavili na kraju prošlog primjera: moguće je gledati ostatke modulo neki  , i ne zaključiti da jednadžba nema rješenja, no svejedno možemo zaključiti nešto o jednadžbi.
, i ne zaključiti da jednadžba nema rješenja, no svejedno možemo zaključiti nešto o jednadžbi.
Primjer.
Odredi sva rješenja jednadžbe 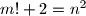 , gdje su
, gdje su  i
i  prirodni brojevi.
prirodni brojevi.
Rješenje.
Za one koji ne znaju, 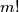 se čita kao em faktorijela i oznaka je za umnožak prvih
se čita kao em faktorijela i oznaka je za umnožak prvih  prirodnih brojeva. Dodatno se definira
prirodnih brojeva. Dodatno se definira 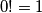 . Dakle,
. Dakle, 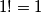 ,
, 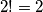 ,
, 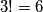 , itd.
, itd.
Zadatci s faktorijelima u pravilu koriste činjenicu da već za male  izraz
izraz 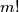 daje ostatak
daje ostatak  pri dijeljenju s mnogim brojevima
pri dijeljenju s mnogim brojevima  , što reducira moguće ostatke koje izrazi u jednadžbi mogu davati pri dijeljenju s
, što reducira moguće ostatke koje izrazi u jednadžbi mogu davati pri dijeljenju s  . Samo treba izabrati onaj
. Samo treba izabrati onaj  za koji ćemo saznati najviše, ovisno o preostalim izrazima u jednadžbi.
za koji ćemo saznati najviše, ovisno o preostalim izrazima u jednadžbi.
S desne strane jednakosti nas čeka potpun kvadrat. Zato ponovno možemo gledati ostatke koje jednadžba daje pri dijeljenju s  . Za
. Za 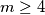 , broj
, broj 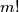 između ostalog u sebi sadrži umnožak brojeva
između ostalog u sebi sadrži umnožak brojeva  i
i  , pa je sigurno djeljiv s
, pa je sigurno djeljiv s  . Zato za takve
. Zato za takve  lijeva strana jednadžbe
lijeva strana jednadžbe 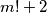 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  . S druge strane, potpun kvadrat
. S druge strane, potpun kvadrat 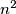 može davati samo ostatke
može davati samo ostatke  ili
ili  pri dijeljenju s
pri dijeljenju s  .
.
Za razliku od prošlog primjera kad smo zaključili da jednadžba uopće nema rješenja, sada zaključujemo da jednadžba nema rješenja u jednom (velikom) slučaju, kada je 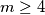 . Preostalo je riješiti jednadžbu kada je
. Preostalo je riješiti jednadžbu kada je 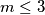 , a to možemo direktnom provjerom. Uvrštavajući brojeve
, a to možemo direktnom provjerom. Uvrštavajući brojeve 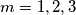 u izraz
u izraz 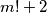 , dobivamo redom
, dobivamo redom 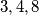 , od kojih je samo
, od kojih je samo  potpun kvadrat. Zato je jedino rješenje ove jednadžbe
potpun kvadrat. Zato je jedino rješenje ove jednadžbe 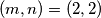 .
.
Ovaj zadatak mogli smo riješiti i gledajući modulo  (za
(za 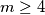 broj
broj 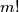 djeljiv je s
djeljiv je s  ), ali i gledajući modulo
), ali i gledajući modulo  (za
(za 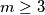 broj
broj 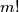 djeljiv je s
djeljiv je s  ). Provjerite kako bi izgledao postupak rješavanja u tim slučajevima.
). Provjerite kako bi izgledao postupak rješavanja u tim slučajevima.
Zadatci u kojima su nepoznanice prosti brojevi imaju velike sličnosti sa zadatcima u kojima se pojavljuju faktorijeli. U takvim zadatcima isto možete gledati izraze modulo neki  , te ako zaključite da je recimo neki prosti broj nužno djeljiv s
, te ako zaključite da je recimo neki prosti broj nužno djeljiv s  , zaključili ste da je taj broj nužno jednak
, zaključili ste da je taj broj nužno jednak  , što je sigurno dobar korak u rješavanju zadatka.
, što je sigurno dobar korak u rješavanju zadatka.
Upišite 1 za nastavak.
Kao što smo najavili na kraju prošlog primjera: moguće je gledati ostatke modulo neki $N$, i ne zaključiti da jednadžba nema rješenja, no svejedno možemo zaključiti nešto o jednadžbi.
\textbf{Primjer.}
Odredi sva rješenja jednadžbe $m!+2=n^2$, gdje su $m$ i $n$ prirodni brojevi.
\textbf{Rješenje.}
Za one koji ne znaju, $m!$ se čita kao \textit{em faktorijela} i oznaka je za umnožak prvih $m$ prirodnih brojeva. Dodatno se definira $0! = 1$. Dakle, $1! = 1$, $2! = 2$, $3! = 6$, itd.
Zadatci s faktorijelima u pravilu koriste činjenicu da već za male $m$ izraz $m!$ daje ostatak $0$ pri dijeljenju s mnogim brojevima $N$, što reducira moguće ostatke koje izrazi u jednadžbi mogu davati pri dijeljenju s $N$. Samo treba izabrati onaj $N$ za koji ćemo saznati najviše, ovisno o preostalim izrazima u jednadžbi.
S desne strane jednakosti nas čeka potpun kvadrat. Zato ponovno možemo gledati ostatke koje jednadžba daje pri dijeljenju s $4$. Za $m \geq 4$, broj $m!$ između ostalog u sebi sadrži umnožak brojeva $2$ i $4$, pa je sigurno djeljiv s $4$. Zato za takve $m$ lijeva strana jednadžbe $m!+2$ daje ostatak $2$ pri dijeljenju s $4$. S druge strane, potpun kvadrat $n^2$ može davati samo ostatke $0$ ili $1$ pri dijeljenju s $4$.
Za razliku od prošlog primjera kad smo zaključili da jednadžba uopće nema rješenja, sada zaključujemo da jednadžba nema rješenja u jednom (velikom) slučaju, kada je $m \geq 4$. Preostalo je riješiti jednadžbu kada je $m \leq 3$, a to možemo direktnom provjerom. Uvrštavajući brojeve $m=1,2,3$ u izraz $m!+2$, dobivamo redom $3,4,8$, od kojih je samo $4$ potpun kvadrat. Zato je jedino rješenje ove jednadžbe $(m,n) = (2,2)$.
Ovaj zadatak mogli smo riješiti i gledajući modulo $8$ (za $m \geq 4$ broj $m!$ djeljiv je s $8$), ali i gledajući modulo $3$ (za $m \geq 3$ broj $m!$ djeljiv je s $3$). Provjerite kako bi izgledao postupak rješavanja u tim slučajevima.
Zadatci u kojima su nepoznanice prosti brojevi imaju velike sličnosti sa zadatcima u kojima se pojavljuju faktorijeli. U takvim zadatcima isto možete gledati izraze modulo neki $N$, te ako zaključite da je recimo neki prosti broj nužno djeljiv s $3$, zaključili ste da je taj broj nužno jednak $3$, što je sigurno dobar korak u rješavanju zadatka.
Upišite 1 za nastavak.
 , i ne zaključiti da jednadžba nema rješenja, no svejedno možemo zaključiti nešto o jednadžbi.
, i ne zaključiti da jednadžba nema rješenja, no svejedno možemo zaključiti nešto o jednadžbi.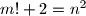 , gdje su
, gdje su  i
i  prirodni brojevi.
prirodni brojevi.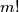 se čita kao em faktorijela i oznaka je za umnožak prvih
se čita kao em faktorijela i oznaka je za umnožak prvih  prirodnih brojeva. Dodatno se definira
prirodnih brojeva. Dodatno se definira 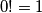 . Dakle,
. Dakle, 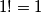 ,
, 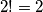 ,
, 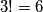 , itd.
, itd. izraz
izraz 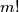 daje ostatak
daje ostatak  pri dijeljenju s mnogim brojevima
pri dijeljenju s mnogim brojevima  , što reducira moguće ostatke koje izrazi u jednadžbi mogu davati pri dijeljenju s
, što reducira moguće ostatke koje izrazi u jednadžbi mogu davati pri dijeljenju s  . Samo treba izabrati onaj
. Samo treba izabrati onaj  za koji ćemo saznati najviše, ovisno o preostalim izrazima u jednadžbi.
za koji ćemo saznati najviše, ovisno o preostalim izrazima u jednadžbi. . Za
. Za 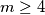 , broj
, broj 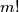 između ostalog u sebi sadrži umnožak brojeva
između ostalog u sebi sadrži umnožak brojeva  i
i  , pa je sigurno djeljiv s
, pa je sigurno djeljiv s  . Zato za takve
. Zato za takve  lijeva strana jednadžbe
lijeva strana jednadžbe 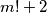 daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  . S druge strane, potpun kvadrat
. S druge strane, potpun kvadrat 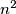 može davati samo ostatke
može davati samo ostatke  ili
ili  pri dijeljenju s
pri dijeljenju s  .
.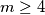 . Preostalo je riješiti jednadžbu kada je
. Preostalo je riješiti jednadžbu kada je 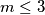 , a to možemo direktnom provjerom. Uvrštavajući brojeve
, a to možemo direktnom provjerom. Uvrštavajući brojeve 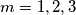 u izraz
u izraz 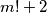 , dobivamo redom
, dobivamo redom 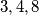 , od kojih je samo
, od kojih je samo  potpun kvadrat. Zato je jedino rješenje ove jednadžbe
potpun kvadrat. Zato je jedino rješenje ove jednadžbe 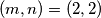 .
. (za
(za 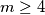 broj
broj 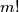 djeljiv je s
djeljiv je s  ), ali i gledajući modulo
), ali i gledajući modulo  (za
(za 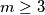 broj
broj 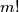 djeljiv je s
djeljiv je s  ). Provjerite kako bi izgledao postupak rješavanja u tim slučajevima.
). Provjerite kako bi izgledao postupak rješavanja u tim slučajevima. , te ako zaključite da je recimo neki prosti broj nužno djeljiv s
, te ako zaključite da je recimo neki prosti broj nužno djeljiv s  , zaključili ste da je taj broj nužno jednak
, zaključili ste da je taj broj nužno jednak  , što je sigurno dobar korak u rješavanju zadatka.
, što je sigurno dobar korak u rješavanju zadatka.