Primjer.
Odredite prirodne brojeve  za koje je
za koje je 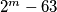 potpun kub prirodnog broja.
potpun kub prirodnog broja.
Rješenje.
Zapišimo prvo ovaj uvjet jednadžbom 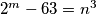 . Brojevi
. Brojevi  i
i  su prirodni. Ako bude bilo bitno, primijetite da možemo zaključiti da je
su prirodni. Ako bude bilo bitno, primijetite da možemo zaključiti da je 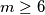 , jer je inače lijeva strana negativna.
, jer je inače lijeva strana negativna.
Ponovno pogledajmo jednadžbu modulo neki  . Iz uputa s početka, zbog člana
. Iz uputa s početka, zbog člana 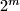 mogli bismo gledati jednadžbu modulo
mogli bismo gledati jednadžbu modulo  ili
ili  , no nećemo se usrećiti budući da
, no nećemo se usrećiti budući da 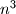 može davati razne ostatke pri dijeljenju s tim brojevima. No,
može davati razne ostatke pri dijeljenju s tim brojevima. No, 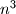 je potpun kub, pa ima smisla gledati ostatke modulo
je potpun kub, pa ima smisla gledati ostatke modulo  .
.
Desna strana daje ostatke  ,
,  ili
ili  pri dijeljenju sa
pri dijeljenju sa  . Broj
. Broj 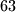 djeljiv je sa
djeljiv je sa  , dok izraz
, dok izraz 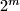 podijeljen sa
podijeljen sa  za razne
za razne 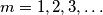 daje ostatke
daje ostatke 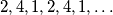 . Da bi jednadžba bila zadovoljena, mora postojati neki izbor ostataka takav da se ostatci na lijevoj i desnoj strani poklapaju. Jedini izbor je kada oba izraza
. Da bi jednadžba bila zadovoljena, mora postojati neki izbor ostataka takav da se ostatci na lijevoj i desnoj strani poklapaju. Jedini izbor je kada oba izraza 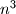 i
i 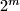 daju ostatak
daju ostatak  pri dijeljenju sa
pri dijeljenju sa  . Dok za
. Dok za  ne saznajemo mnogo (preciznije, možemo samo zaključiti da to znači da
ne saznajemo mnogo (preciznije, možemo samo zaključiti da to znači da  daje ostatak
daje ostatak  ,
,  ili
ili  pri dijeljenju sa
pri dijeljenju sa  ), za
), za 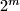 primjećujemo da se ostatak
primjećujemo da se ostatak  pojavljuje na svakom trećem mjestu u nizu ostataka
pojavljuje na svakom trećem mjestu u nizu ostataka 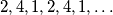 koje
koje 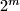 daje podijeljen sa
daje podijeljen sa  . Zato možemo zaključiti da je
. Zato možemo zaključiti da je  nužno djeljiv s
nužno djeljiv s  , odnosno možemo pisati
, odnosno možemo pisati 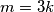 , za neki prirodan broj
, za neki prirodan broj  .
.
To je mnogo slabiji zaključak nego u prošlom primjeru u vidu da nismo zadatak reducirali na konačno mnogo slučajeva koje treba provjeriti. Samo smo zaključili da je  djeljiv s
djeljiv s  . No, i to je veliki korak, kada se sjetimo drugih tehnika za rješavanje diofantskih jednadžbi.
. No, i to je veliki korak, kada se sjetimo drugih tehnika za rješavanje diofantskih jednadžbi.
Uvrstimo ovaj zaključak u početnu jednadžbu: 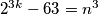 . Na obje strane jednadžbe imamo potpun kub. Kada zapišemo jednadžbu drugačije, možemo iskoristiti razliku kubova i faktorizirati izraz:
. Na obje strane jednadžbe imamo potpun kub. Kada zapišemo jednadžbu drugačije, možemo iskoristiti razliku kubova i faktorizirati izraz: 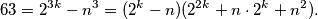 Slijeve strane imamo broj
Slijeve strane imamo broj 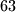 koji nudi konačno mnogo različitih faktorizacija:
koji nudi konačno mnogo različitih faktorizacija: 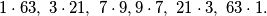
Zato imamo šest mogućih podslučajeva: 
Za svaku od tih kombinacija treba provjeriti vodi li ka rješenju za neke prirodne  i
i  .
.
U prvom slučaju bismo iz prve jednakosti imamo izrazili  te uvrstili u drugu. Dobili bismo
te uvrstili u drugu. Dobili bismo 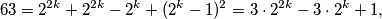 što nema rješenja jer možemo gledati jednadžbu modulo
što nema rješenja jer možemo gledati jednadžbu modulo  : svi izrazi osim zadnje jedinice djeljivi su s
: svi izrazi osim zadnje jedinice djeljivi su s  .
.
U drugom slučaju ponovno uvrštavmo  iz prve u drugu jednakost i dobivamo
iz prve u drugu jednakost i dobivamo 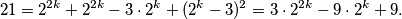 Rješavanjem kvadratne jednadžbe po
Rješavanjem kvadratne jednadžbe po 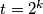 dobivamo rješenja
dobivamo rješenja 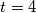 i
i 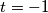 , odakle je
, odakle je 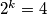 , odnosno
, odnosno 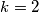 , tj.
, tj. 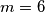 i
i 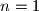 .
.
U trećem slučaju analogno dobivamo 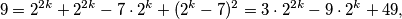 a ta jednadžba ponovno nema rješenja ako gledamo jednadžbu modulo
a ta jednadžba ponovno nema rješenja ako gledamo jednadžbu modulo  .
.
Da bismo u potpunosti riješili zadatak, treba provjeriti i preostala 3 slučaja. U tim slučajevima nećemo dobiti nova rješenja.
Umjesto dodatnog gledanja preostala  slučaja, broj slučajeva mogli bismo prepoloviti. Naime, primijetimo da obje zagrade
slučaja, broj slučajeva mogli bismo prepoloviti. Naime, primijetimo da obje zagrade 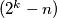 i
i 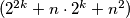 trebaju biti pozitivni brojevi (jer je druga zbroj prirodnih brojeva, a umnožak im mora biti pozitivan), te da je druga zagrada sigurno veća od druge jer vrijedi
trebaju biti pozitivni brojevi (jer je druga zbroj prirodnih brojeva, a umnožak im mora biti pozitivan), te da je druga zagrada sigurno veća od druge jer vrijedi 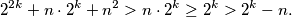 Zato ne treba gledati one mogućnosti u kojima je drugi faktor u umnošku manji od prvog, tj. preostala
Zato ne treba gledati one mogućnosti u kojima je drugi faktor u umnošku manji od prvog, tj. preostala  slučaja.
slučaja.
Upišite 1 za nastavak.
\textbf{Primjer.}
Odredite prirodne brojeve $m$ za koje je $2^m-63$ potpun kub prirodnog broja.
\textbf{Rješenje.}
Zapišimo prvo ovaj uvjet jednadžbom $2^m - 63 = n^3$. Brojevi $m$ i $n$ su prirodni. Ako bude bilo bitno, primijetite da možemo zaključiti da je $m \geq 6$, jer je inače lijeva strana negativna.
Ponovno pogledajmo jednadžbu modulo neki $N$. Iz uputa s početka, zbog člana $2^m$ mogli bismo gledati jednadžbu modulo $4$ ili $8$, no nećemo se usrećiti budući da $n^3$ može davati razne ostatke pri dijeljenju s tim brojevima. No, $n^3$ je potpun kub, pa ima smisla gledati ostatke modulo $7$.
Desna strana daje ostatke $0$, $1$ ili $6$ pri dijeljenju sa $7$. Broj $63$ djeljiv je sa $7$, dok izraz $2^m$ podijeljen sa $7$ za razne $m=1,2,3,\dots$ daje ostatke
$ 2, 4, 1, 2, 4, 1, \dots$.
Da bi jednadžba bila zadovoljena, mora postojati neki izbor ostataka takav da se ostatci na lijevoj i desnoj strani poklapaju. Jedini izbor je kada oba izraza $n^3$ i $2^m$ daju ostatak $1$ pri dijeljenju sa $7$. Dok za $n$ ne saznajemo mnogo (preciznije, možemo samo zaključiti da to znači da $n$ daje ostatak $1$, $2$ ili $4$ pri dijeljenju sa $7$), za $2^m$ primjećujemo da se ostatak $1$ pojavljuje na svakom trećem mjestu u nizu ostataka $ 2, 4, 1, 2, 4, 1, \dots$ koje $2^m$ daje podijeljen sa $7$. Zato možemo zaključiti da je $m$ nužno djeljiv s $3$, odnosno možemo pisati $m=3k$, za neki prirodan broj $k$.
To je mnogo slabiji zaključak nego u prošlom primjeru u vidu da nismo zadatak reducirali na konačno mnogo slučajeva koje treba provjeriti. Samo smo zaključili da je $m$ djeljiv s $3$. No, i to je veliki korak, kada se sjetimo drugih tehnika za rješavanje diofantskih jednadžbi.
Uvrstimo ovaj zaključak u početnu jednadžbu: $2^{3k} - 63 = n^3$. Na obje strane jednadžbe imamo potpun kub. Kada zapišemo jednadžbu drugačije, možemo iskoristiti razliku kubova i faktorizirati izraz:
\[ 63 = 2^{3k} - n^3 = (2^k - n) (2^{2k} + n \cdot 2^k + n^2 ).\]
Slijeve strane imamo broj $63$ koji nudi konačno mnogo različitih faktorizacija:
\[ 1\cdot 63, \ 3 \cdot 21, \ 7 \cdot 9, 9\cdot 7, \ 21 \cdot 3, \ 63 \cdot 1 .\]
Zato imamo šest mogućih podslučajeva:
\begin{itemize}
\item $2^k - n = 1$, $2^{2k} + n \cdot 2^k + n^2 = 63$;
\item $2^k - n = 3$, $2^{2k} + n \cdot 2^k + n^2 = 21$;
\item $2^k - n = 7$, $2^{2k} + n \cdot 2^k + n^2 = 9$;
\item $2^k - n = 9$, $2^{2k} + n \cdot 2^k + n^2 = 7$;
\item $2^k - n = 21$, $2^{2k} + n \cdot 2^k + n^2 = 3$;
\item $2^k - n = 63$, $2^{2k} + n \cdot 2^k + n^2 = 1$.
\end{itemize}
Za svaku od tih kombinacija treba provjeriti vodi li ka rješenju za neke prirodne $k$ i $n$.
U prvom slučaju bismo iz prve jednakosti imamo izrazili $n$ te uvrstili u drugu. Dobili bismo
\[ 63 = 2^{2k} + 2^{2k} - 2^k + (2^k - 1)^2 = 3 \cdot 2^{2k} - 3 \cdot 2^k +1,\]
što nema rješenja jer možemo gledati jednadžbu modulo $3$: svi izrazi osim zadnje jedinice djeljivi su s $3$.
U drugom slučaju ponovno uvrštavmo $n$ iz prve u drugu jednakost i dobivamo
\[ 21 = 2^{2k} + 2^{2k} - 3 \cdot 2^k + (2^k - 3)^2 = 3 \cdot 2^{2k} - 9 \cdot 2^k + 9.\] Rješavanjem kvadratne jednadžbe po $t = 2^k$ dobivamo rješenja $t = 4$ i $t = -1$, odakle je $2^ k = 4$, odnosno $k=2$, tj. $m=6$ i $n = 1$.
U trećem slučaju analogno dobivamo
\[ 9 = 2^{2k} + 2^{2k} - 7 \cdot 2^k + (2^k - 7)^2 = 3 \cdot 2^{2k} - 9 \cdot 2^k + 49,\]
a ta jednadžba ponovno nema rješenja ako gledamo jednadžbu modulo $3$.
Da bismo u potpunosti riješili zadatak, treba provjeriti i preostala 3 slučaja. U tim slučajevima nećemo dobiti nova rješenja.
Umjesto dodatnog gledanja preostala $3$ slučaja, broj slučajeva mogli bismo prepoloviti. Naime, primijetimo da obje zagrade $(2^k - n)$ i $ (2^{2k} + n \cdot 2^k + n^2 )$ trebaju biti pozitivni brojevi (jer je druga zbroj prirodnih brojeva, a umnožak im mora biti pozitivan), te da je druga zagrada sigurno veća od druge jer vrijedi
\[ 2^{2k} + n \cdot 2^k + n^2 > n \cdot 2^k \geq 2^k > 2^k - n.\]
Zato ne treba gledati one mogućnosti u kojima je drugi faktor u umnošku manji od prvog, tj. preostala $3$ slučaja.
Upišite 1 za nastavak.
 za koje je
za koje je 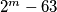 potpun kub prirodnog broja.
potpun kub prirodnog broja.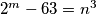 . Brojevi
. Brojevi  i
i  su prirodni. Ako bude bilo bitno, primijetite da možemo zaključiti da je
su prirodni. Ako bude bilo bitno, primijetite da možemo zaključiti da je 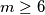 , jer je inače lijeva strana negativna.
, jer je inače lijeva strana negativna. . Iz uputa s početka, zbog člana
. Iz uputa s početka, zbog člana 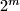 mogli bismo gledati jednadžbu modulo
mogli bismo gledati jednadžbu modulo  ili
ili  , no nećemo se usrećiti budući da
, no nećemo se usrećiti budući da 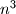 može davati razne ostatke pri dijeljenju s tim brojevima. No,
može davati razne ostatke pri dijeljenju s tim brojevima. No, 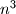 je potpun kub, pa ima smisla gledati ostatke modulo
je potpun kub, pa ima smisla gledati ostatke modulo  .
. ,
,  ili
ili  pri dijeljenju sa
pri dijeljenju sa  . Broj
. Broj 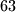 djeljiv je sa
djeljiv je sa  , dok izraz
, dok izraz 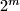 podijeljen sa
podijeljen sa  za razne
za razne 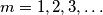 daje ostatke
daje ostatke 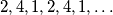 . Da bi jednadžba bila zadovoljena, mora postojati neki izbor ostataka takav da se ostatci na lijevoj i desnoj strani poklapaju. Jedini izbor je kada oba izraza
. Da bi jednadžba bila zadovoljena, mora postojati neki izbor ostataka takav da se ostatci na lijevoj i desnoj strani poklapaju. Jedini izbor je kada oba izraza 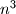 i
i 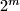 daju ostatak
daju ostatak  pri dijeljenju sa
pri dijeljenju sa  . Dok za
. Dok za  ne saznajemo mnogo (preciznije, možemo samo zaključiti da to znači da
ne saznajemo mnogo (preciznije, možemo samo zaključiti da to znači da  daje ostatak
daje ostatak  ,
,  ili
ili  pri dijeljenju sa
pri dijeljenju sa  ), za
), za 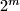 primjećujemo da se ostatak
primjećujemo da se ostatak  pojavljuje na svakom trećem mjestu u nizu ostataka
pojavljuje na svakom trećem mjestu u nizu ostataka 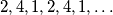 koje
koje 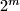 daje podijeljen sa
daje podijeljen sa  . Zato možemo zaključiti da je
. Zato možemo zaključiti da je  nužno djeljiv s
nužno djeljiv s  , odnosno možemo pisati
, odnosno možemo pisati 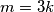 , za neki prirodan broj
, za neki prirodan broj  .
. djeljiv s
djeljiv s  . No, i to je veliki korak, kada se sjetimo drugih tehnika za rješavanje diofantskih jednadžbi.
. No, i to je veliki korak, kada se sjetimo drugih tehnika za rješavanje diofantskih jednadžbi.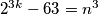 . Na obje strane jednadžbe imamo potpun kub. Kada zapišemo jednadžbu drugačije, možemo iskoristiti razliku kubova i faktorizirati izraz:
. Na obje strane jednadžbe imamo potpun kub. Kada zapišemo jednadžbu drugačije, možemo iskoristiti razliku kubova i faktorizirati izraz: 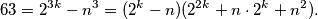 Slijeve strane imamo broj
Slijeve strane imamo broj 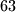 koji nudi konačno mnogo različitih faktorizacija:
koji nudi konačno mnogo različitih faktorizacija: 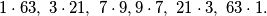

 i
i  .
. te uvrstili u drugu. Dobili bismo
te uvrstili u drugu. Dobili bismo 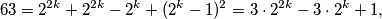 što nema rješenja jer možemo gledati jednadžbu modulo
što nema rješenja jer možemo gledati jednadžbu modulo  : svi izrazi osim zadnje jedinice djeljivi su s
: svi izrazi osim zadnje jedinice djeljivi su s  .
. iz prve u drugu jednakost i dobivamo
iz prve u drugu jednakost i dobivamo 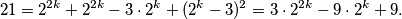 Rješavanjem kvadratne jednadžbe po
Rješavanjem kvadratne jednadžbe po 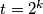 dobivamo rješenja
dobivamo rješenja 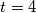 i
i 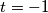 , odakle je
, odakle je 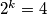 , odnosno
, odnosno 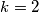 , tj.
, tj. 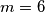 i
i 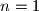 .
.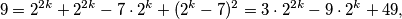 a ta jednadžba ponovno nema rješenja ako gledamo jednadžbu modulo
a ta jednadžba ponovno nema rješenja ako gledamo jednadžbu modulo  .
. slučaja, broj slučajeva mogli bismo prepoloviti. Naime, primijetimo da obje zagrade
slučaja, broj slučajeva mogli bismo prepoloviti. Naime, primijetimo da obje zagrade 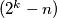 i
i 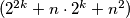 trebaju biti pozitivni brojevi (jer je druga zbroj prirodnih brojeva, a umnožak im mora biti pozitivan), te da je druga zagrada sigurno veća od druge jer vrijedi
trebaju biti pozitivni brojevi (jer je druga zbroj prirodnih brojeva, a umnožak im mora biti pozitivan), te da je druga zagrada sigurno veća od druge jer vrijedi 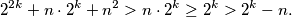 Zato ne treba gledati one mogućnosti u kojima je drugi faktor u umnošku manji od prvog, tj. preostala
Zato ne treba gledati one mogućnosti u kojima je drugi faktor u umnošku manji od prvog, tj. preostala  slučaja.
slučaja.