Pogledajmo još jedan primjer koji će biti malo kompliciraniji od prošlog.
Primjer.
Odredite sve prirodne brojeve  i
i  takve da je
takve da je 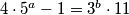 .
.
Rješenje.
Kao u svim zadatcima u ovoj lekciji, počet ćemo s gledanjem ove jednadžbe modulo neki  . Ovo je i inače dobar način kako početi rješavati diofantske jednadžbe: gledati jednadžbu modulo
. Ovo je i inače dobar način kako početi rješavati diofantske jednadžbe: gledati jednadžbu modulo  na natjecanju nije vremenski skupo, a može donijeti neke korisne zaključke za kasnije.
na natjecanju nije vremenski skupo, a može donijeti neke korisne zaključke za kasnije.
U jednadžbi se pojavljuju samo potencije brojeva, nemamo potpune kvadrate ili kubove, tako da su kandidati za  brojevi
brojevi  ,
,  ,
,  ,
,  , ili možda potencije tih brojeva.
, ili možda potencije tih brojeva.
Pogledajmo jednadžbu modulo  . Desna strana jednadžbe je djeljiva s
. Desna strana jednadžbe je djeljiva s  , pa mora i desna, a za to trebamo imati da
, pa mora i desna, a za to trebamo imati da 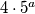 daje ostatak jedan pri dijeljenju s
daje ostatak jedan pri dijeljenju s  . Raspisom za male
. Raspisom za male  primjećujemo da se tom izrazu izmijenjuju ostatci
primjećujemo da se tom izrazu izmijenjuju ostatci  i
i  , pa je nužno
, pa je nužno  paran broj.
paran broj.
Možemo gledati jednadžbu i modulo  ,
,  te
te  . Dobili bismo da je
. Dobili bismo da je  paran,
paran,  daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  i
i  daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  redom. No nijedan zaključak neće biti tako bitan kao onaj da je
redom. No nijedan zaključak neće biti tako bitan kao onaj da je  paran.
paran.
Kako je  paran broj, možemo pisati
paran broj, možemo pisati 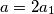 , pa je
, pa je 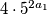 potpun kvadrat. Uz njega se nalazi
potpun kvadrat. Uz njega se nalazi  , što nas poziva da napravimo razliku kvadrata. Dobivamo jednadžbu
, što nas poziva da napravimo razliku kvadrata. Dobivamo jednadžbu 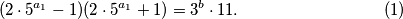 Koraci koje smo radili do sada isti su kao u prošlom primjeru, i česti su u zadatcima ovakvog tipa: prvo modularnom aritmetikom nešto zaključimo o nepoznanicama u jednadžbi što nam pomaže da jednadžbu faktoriziramo.
Koraci koje smo radili do sada isti su kao u prošlom primjeru, i česti su u zadatcima ovakvog tipa: prvo modularnom aritmetikom nešto zaključimo o nepoznanicama u jednadžbi što nam pomaže da jednadžbu faktoriziramo.
Ono što se razlikuje u ovom primjeru je to što umnožak naših nepoznatih faktora je broj koji opet ovisi o nepoznanici, a ne fiksan broj s fiksnom faktorizacijom (ili konačnim brojem mogućnosti faktorizacije). U ovakvim zadatcima korisno je pogledati najveću zajedničku mjeru faktora na lijevoj strani jednadžbe.
Faktori u zagradama 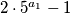 i
i 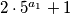 uzastopni su neparni brojevi, pa su zato relativno prosti. Njihov umnožak djeljiv je s
uzastopni su neparni brojevi, pa su zato relativno prosti. Njihov umnožak djeljiv je s 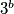 , no kako su relativno prosti, ne mogu oba biti djeljiva s
, no kako su relativno prosti, ne mogu oba biti djeljiva s  . Dakle, jedan od njih mora "preuzeti na sebe" cijeli faktor
. Dakle, jedan od njih mora "preuzeti na sebe" cijeli faktor 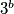 . Slično, ali jednostavnije, ne mogu oba faktora biti djeljiva s
. Slično, ali jednostavnije, ne mogu oba faktora biti djeljiva s  , nego je točno jedan od njih djeljiv s
, nego je točno jedan od njih djeljiv s  .
.
Iz prošlog paragrafa zaključujemo 4 slučaja: 
U prvom slučaju iz prve jednakosti dobivamo 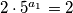 , što nema rješenja u prirodnim brojevima. U drugom slučaju iz prve jednakosti dobivamo
, što nema rješenja u prirodnim brojevima. U drugom slučaju iz prve jednakosti dobivamo 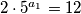 , što također nema rješenja u prirodnim brojevima (jer lijeva strana nije djeljiva s
, što također nema rješenja u prirodnim brojevima (jer lijeva strana nije djeljiva s  , dok desna jest.
, dok desna jest.
U trećem slučaju iz druge jednakosti dobivamo 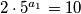 , što daje rješenje
, što daje rješenje 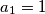 , odnosno
, odnosno 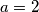 . Lako iz prve jednakosti vidimo da je to zadovoljeno s
. Lako iz prve jednakosti vidimo da je to zadovoljeno s  . U četvrtom slučaju imamo
. U četvrtom slučaju imamo 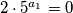 , što ponovno nema rješenja u prirodnim brojevima.
, što ponovno nema rješenja u prirodnim brojevima.
Zato je jedino rješenje jednadžbe 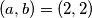 .
.
Vratimo se ponovno na jednadžbu (1). Ona je oblika 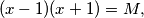 gdje je
gdje je  neki možda nepoznati broj. Za one koji žele znati još više, prokomentirajmo što se još inače može dogoditi u ovakvoj jednadžbi. Iz prirode broja
neki možda nepoznati broj. Za one koji žele znati još više, prokomentirajmo što se još inače može dogoditi u ovakvoj jednadžbi. Iz prirode broja  u našem slučaju znali smo da su faktori
u našem slučaju znali smo da su faktori  i
i  relativno prosti. No, možda inače to ne možemo zaključiti. U takvim slučajevima provodimo Euklidov algoritam na tim faktorima. Drugim riječima, ako je
relativno prosti. No, možda inače to ne možemo zaključiti. U takvim slučajevima provodimo Euklidov algoritam na tim faktorima. Drugim riječima, ako je  najveća zajednička mjera faktora
najveća zajednička mjera faktora  i
i  , budući da
, budući da  dijeli svakog od tih faktora, posebno vrijedi da
dijeli svakog od tih faktora, posebno vrijedi da  dijeli razliku tih brojeva:
dijeli razliku tih brojeva: 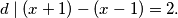 Dakle,
Dakle, 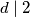 , pa su jedine mogućnosti za
, pa su jedine mogućnosti za 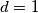 i
i 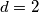 . Ovo u nekim zadatcima može voditi na dva slučaja. U prvom, kao što smo imali u prošlom zadatku, faktori
. Ovo u nekim zadatcima može voditi na dva slučaja. U prvom, kao što smo imali u prošlom zadatku, faktori  i
i  imaju zajedničku mjeru
imaju zajedničku mjeru  , dakle relativno su prosti i umnožak im je
, dakle relativno su prosti i umnožak im je  . U drugom slučaju,
. U drugom slučaju,  i
i  imaju zajedničku mjeru
imaju zajedničku mjeru  . Posebno, oba su parna, pa su zato
. Posebno, oba su parna, pa su zato 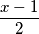 i
i 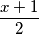 relativno prosti brojevi čiji je umnožak jednak
relativno prosti brojevi čiji je umnožak jednak 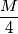 . U oba slučaja na lijevoj strani jednakosti sada imamo umnožak relativno prostih brojeva.
. U oba slučaja na lijevoj strani jednakosti sada imamo umnožak relativno prostih brojeva.
Ako znamo rastav broja  na proste faktore kao u prošlom zadatku, sada možemo zaključiti da je svaka potencija prostog broja nužno sadržana u točno jednom od faktora s lijeve strane. Postoje zadatci i u kojima je
na proste faktore kao u prošlom zadatku, sada možemo zaključiti da je svaka potencija prostog broja nužno sadržana u točno jednom od faktora s lijeve strane. Postoje zadatci i u kojima je  još manje poznatog oblika, recimo, samo znamo da je potpun kvadrat ili potpun kub. Tada koristimo tvrdnju: ako je umnožak relativno prostih brojeva
još manje poznatog oblika, recimo, samo znamo da je potpun kvadrat ili potpun kub. Tada koristimo tvrdnju: ako je umnožak relativno prostih brojeva  i
i  potpun kvadrat / kub, tada je svaki od brojeva
potpun kvadrat / kub, tada je svaki od brojeva  i
i  potpun kvadrat / kub. Tvrdnja naravno vrijedi i za više potencije.
potpun kvadrat / kub. Tvrdnja naravno vrijedi i za više potencije.
Svođenje zadatka na podslučajeve približavate se konačnom rješenju zadatka jer je svaki od tih podslučajeva lakši od originalnog zadatka, barem u pravilu. Neki slučajevi mogu biti trivijalni (kao što smo vidjeli u prošlom zadatku, kada smo imali jednakost oblika 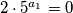 ), a ponekad možemo dobiti jedan novi mali zadatak kojem pristupamo kao i originalnom zadatku: modularna aritmetika, faktorizacija, eventualno traženje mjere i sl.
), a ponekad možemo dobiti jedan novi mali zadatak kojem pristupamo kao i originalnom zadatku: modularna aritmetika, faktorizacija, eventualno traženje mjere i sl.
Ovaj kraj lekcije pokriva neke hipotetske situacije koji se mogu pojaviti u zadatcima. Zadatci u lancima za samostalno rješavanje ne bi trebali imati ovakve situacije i sličniji su uvodnim primjerima, te vas pozivamo da ih sami riješite.
Upišite 1 za nastavak.
Pogledajmo još jedan primjer koji će biti malo kompliciraniji od prošlog.
\textbf{Primjer.}
Odredite sve prirodne brojeve $a$ i $b$ takve da je
$4 \cdot 5 ^a -1 = 3^b \cdot 11$.
\textbf{Rješenje.}
Kao u svim zadatcima u ovoj lekciji, počet ćemo s gledanjem ove jednadžbe modulo neki $N$. Ovo je i inače dobar način kako početi rješavati diofantske jednadžbe: gledati jednadžbu modulo $N$ na natjecanju nije vremenski skupo, a može donijeti neke korisne zaključke za kasnije.
U jednadžbi se pojavljuju samo potencije brojeva, nemamo potpune kvadrate ili kubove, tako da su kandidati za $N$ brojevi $3$, $4$, $5$, $11$, ili možda potencije tih brojeva.
Pogledajmo jednadžbu modulo $3$. Desna strana jednadžbe je djeljiva s $3$, pa mora i desna, a za to trebamo imati da $4 \cdot 5 ^a $ daje ostatak jedan pri dijeljenju s $3$. Raspisom za male $a$ primjećujemo da se tom izrazu izmijenjuju ostatci $2$ i $1$, pa je nužno $a$ paran broj.
Možemo gledati jednadžbu i modulo $4$, $5$ te $11$. Dobili bismo da je $b$ paran, $b$ daje ostatak $2$ pri dijeljenju s $4$ i $a$ daje ostatak $2$ pri dijeljenju s $4$ redom. No nijedan zaključak neće biti tako bitan kao onaj da je $a$ paran.
Kako je $a$ paran broj, možemo pisati $a=2a_1$, pa je $4 \cdot 5^{2a_1}$ potpun kvadrat. Uz njega se nalazi $-1$, što nas poziva da napravimo razliku kvadrata. Dobivamo jednadžbu
\begin{equation}\label{eq1}
(2 \cdot 5^{a_1} -1 )(2 \cdot 5^{a_1} +1 ) = 3^b \cdot 11 .
\end{equation}
Koraci koje smo radili do sada isti su kao u prošlom primjeru, i česti su u zadatcima ovakvog tipa: prvo modularnom aritmetikom nešto zaključimo o nepoznanicama u jednadžbi što nam pomaže da jednadžbu faktoriziramo.
Ono što se razlikuje u ovom primjeru je to što umnožak naših nepoznatih faktora je broj koji opet ovisi o nepoznanici, a ne fiksan broj s fiksnom faktorizacijom (ili konačnim brojem mogućnosti faktorizacije). U ovakvim zadatcima korisno je pogledati najveću zajedničku mjeru faktora na lijevoj strani jednadžbe.
Faktori u zagradama $2 \cdot 5^{a_1} -1$ i $2 \cdot 5^{a_1} +1 $ uzastopni su neparni brojevi, pa su zato relativno prosti. Njihov umnožak djeljiv je s $3^b$, no kako su relativno prosti, ne mogu oba biti djeljiva s $3$. Dakle, jedan od njih mora "preuzeti na sebe" cijeli faktor $3^b$. Slično, ali jednostavnije, ne mogu oba faktora biti djeljiva s $11$, nego je točno jedan od njih djeljiv s $11$.
Iz prošlog paragrafa zaključujemo 4 slučaja:
\begin{itemize}
\item $2 \cdot 5^{a_1} -1 = 1$, $2 \cdot 5^{a_1} +1 = 3^b \cdot 11$;
\item $2 \cdot 5^{a_1} -1 = 11$, $2 \cdot 5^{a_1} +1 = 3^b $;
\item $2 \cdot 5^{a_1} -1 = 3^b$, $2 \cdot 5^{a_1} +1 = 11 $;
\item $2 \cdot 5^{a_1} -1 = 3^b \cdot 11 $, $2 \cdot 5^{a_1} +1 = 1 $.
\end{itemize}
U prvom slučaju iz prve jednakosti dobivamo $2 \cdot 5^{a_1} = 2$, što nema rješenja u prirodnim brojevima. U drugom slučaju iz prve jednakosti dobivamo $2 \cdot 5^{a_1} = 12$, što također nema rješenja u prirodnim brojevima (jer lijeva strana nije djeljiva s $3$, dok desna jest.
U trećem slučaju iz druge jednakosti dobivamo $2 \cdot 5^{a_1} = 10$, što daje rješenje $a_1 = 1$, odnosno $a=2$. Lako iz prve jednakosti vidimo da je to zadovoljeno s $b=2$. U četvrtom slučaju imamo $2 \cdot 5^{a_1} = 0$, što ponovno nema rješenja u prirodnim brojevima.
Zato je jedino rješenje jednadžbe $(a,b) = (2,2)$.
Vratimo se ponovno na jednadžbu \textbf{(1)}. Ona je oblika
\[ (x-1) (x+1) = M, \]
gdje je $M$ neki možda nepoznati broj.
Za one koji žele znati još više, prokomentirajmo što se još inače može dogoditi u ovakvoj jednadžbi. Iz prirode broja $x$ u našem slučaju znali smo da su faktori $x-1$ i $x+1$ relativno prosti. No, možda inače to ne možemo zaključiti. U takvim slučajevima provodimo Euklidov algoritam na tim faktorima. Drugim riječima, ako je $d$ najveća zajednička mjera faktora $x-1$ i $x+1$, budući da $d$ dijeli svakog od tih faktora, posebno vrijedi da $d$ dijeli razliku tih brojeva:
\[ d\mid (x+1) - (x-1) = 2.\]
Dakle, $d\mid 2$, pa su jedine mogućnosti za $d=1$ i $d=2$. Ovo u nekim zadatcima može voditi na dva slučaja. U prvom, kao što smo imali u prošlom zadatku, faktori $x-1$ i $x+1$ imaju zajedničku mjeru $1$, dakle relativno su prosti i umnožak im je $M$. U drugom slučaju, $x-1$ i $x+1$ imaju zajedničku mjeru $2$. Posebno, oba su parna, pa su zato $\dfrac{x-1}2$ i $\dfrac{x+1}2$ relativno prosti brojevi čiji je umnožak jednak $\dfrac M4$. U oba slučaja na lijevoj strani jednakosti sada imamo umnožak relativno prostih brojeva.
Ako znamo rastav broja $M$ na proste faktore kao u prošlom zadatku, sada možemo zaključiti da je svaka potencija prostog broja nužno sadržana u točno jednom od faktora s lijeve strane. Postoje zadatci i u kojima je $M$ još manje poznatog oblika, recimo, samo znamo da je potpun kvadrat ili potpun kub. Tada koristimo tvrdnju: \textit{ako je umnožak relativno prostih brojeva $m$ i $n$ potpun kvadrat / kub, tada je svaki od brojeva $m$ i $n$ potpun kvadrat / kub}. Tvrdnja naravno vrijedi i za više potencije.
Svođenje zadatka na podslučajeve približavate se konačnom rješenju zadatka jer je svaki od tih podslučajeva lakši od originalnog zadatka, barem u pravilu. Neki slučajevi mogu biti trivijalni (kao što smo vidjeli u prošlom zadatku, kada smo imali jednakost oblika $2 \cdot 5^{a_1} = 0$), a ponekad možemo dobiti jedan novi mali zadatak kojem pristupamo kao i originalnom zadatku: modularna aritmetika, faktorizacija, eventualno traženje mjere i sl.
Ovaj kraj lekcije pokriva neke hipotetske situacije koji se mogu pojaviti u zadatcima. Zadatci u lancima za samostalno rješavanje ne bi trebali imati ovakve situacije i sličniji su uvodnim primjerima, te vas pozivamo da ih sami riješite.
Upišite 1 za nastavak.
 i
i  takve da je
takve da je 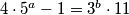 .
. . Ovo je i inače dobar način kako početi rješavati diofantske jednadžbe: gledati jednadžbu modulo
. Ovo je i inače dobar način kako početi rješavati diofantske jednadžbe: gledati jednadžbu modulo  na natjecanju nije vremenski skupo, a može donijeti neke korisne zaključke za kasnije.
na natjecanju nije vremenski skupo, a može donijeti neke korisne zaključke za kasnije. brojevi
brojevi  ,
,  ,
,  ,
,  , ili možda potencije tih brojeva.
, ili možda potencije tih brojeva. . Desna strana jednadžbe je djeljiva s
. Desna strana jednadžbe je djeljiva s  , pa mora i desna, a za to trebamo imati da
, pa mora i desna, a za to trebamo imati da 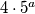 daje ostatak jedan pri dijeljenju s
daje ostatak jedan pri dijeljenju s  . Raspisom za male
. Raspisom za male  primjećujemo da se tom izrazu izmijenjuju ostatci
primjećujemo da se tom izrazu izmijenjuju ostatci  i
i  , pa je nužno
, pa je nužno  paran broj.
paran broj. ,
,  te
te  . Dobili bismo da je
. Dobili bismo da je  paran,
paran,  daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  i
i  daje ostatak
daje ostatak  pri dijeljenju s
pri dijeljenju s  redom. No nijedan zaključak neće biti tako bitan kao onaj da je
redom. No nijedan zaključak neće biti tako bitan kao onaj da je  paran.
paran. paran broj, možemo pisati
paran broj, možemo pisati 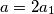 , pa je
, pa je 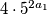 potpun kvadrat. Uz njega se nalazi
potpun kvadrat. Uz njega se nalazi  , što nas poziva da napravimo razliku kvadrata. Dobivamo jednadžbu
, što nas poziva da napravimo razliku kvadrata. Dobivamo jednadžbu 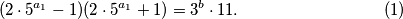 Koraci koje smo radili do sada isti su kao u prošlom primjeru, i česti su u zadatcima ovakvog tipa: prvo modularnom aritmetikom nešto zaključimo o nepoznanicama u jednadžbi što nam pomaže da jednadžbu faktoriziramo.
Koraci koje smo radili do sada isti su kao u prošlom primjeru, i česti su u zadatcima ovakvog tipa: prvo modularnom aritmetikom nešto zaključimo o nepoznanicama u jednadžbi što nam pomaže da jednadžbu faktoriziramo.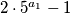 i
i 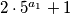 uzastopni su neparni brojevi, pa su zato relativno prosti. Njihov umnožak djeljiv je s
uzastopni su neparni brojevi, pa su zato relativno prosti. Njihov umnožak djeljiv je s 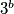 , no kako su relativno prosti, ne mogu oba biti djeljiva s
, no kako su relativno prosti, ne mogu oba biti djeljiva s  . Dakle, jedan od njih mora "preuzeti na sebe" cijeli faktor
. Dakle, jedan od njih mora "preuzeti na sebe" cijeli faktor 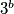 . Slično, ali jednostavnije, ne mogu oba faktora biti djeljiva s
. Slično, ali jednostavnije, ne mogu oba faktora biti djeljiva s  , nego je točno jedan od njih djeljiv s
, nego je točno jedan od njih djeljiv s  .
.
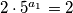 , što nema rješenja u prirodnim brojevima. U drugom slučaju iz prve jednakosti dobivamo
, što nema rješenja u prirodnim brojevima. U drugom slučaju iz prve jednakosti dobivamo 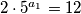 , što također nema rješenja u prirodnim brojevima (jer lijeva strana nije djeljiva s
, što također nema rješenja u prirodnim brojevima (jer lijeva strana nije djeljiva s  , dok desna jest.
, dok desna jest.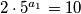 , što daje rješenje
, što daje rješenje 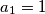 , odnosno
, odnosno 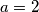 . Lako iz prve jednakosti vidimo da je to zadovoljeno s
. Lako iz prve jednakosti vidimo da je to zadovoljeno s  . U četvrtom slučaju imamo
. U četvrtom slučaju imamo 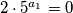 , što ponovno nema rješenja u prirodnim brojevima.
, što ponovno nema rješenja u prirodnim brojevima.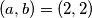 .
.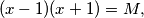 gdje je
gdje je  neki možda nepoznati broj. Za one koji žele znati još više, prokomentirajmo što se još inače može dogoditi u ovakvoj jednadžbi. Iz prirode broja
neki možda nepoznati broj. Za one koji žele znati još više, prokomentirajmo što se još inače može dogoditi u ovakvoj jednadžbi. Iz prirode broja  u našem slučaju znali smo da su faktori
u našem slučaju znali smo da su faktori  i
i  relativno prosti. No, možda inače to ne možemo zaključiti. U takvim slučajevima provodimo Euklidov algoritam na tim faktorima. Drugim riječima, ako je
relativno prosti. No, možda inače to ne možemo zaključiti. U takvim slučajevima provodimo Euklidov algoritam na tim faktorima. Drugim riječima, ako je  najveća zajednička mjera faktora
najveća zajednička mjera faktora  i
i  , budući da
, budući da  dijeli svakog od tih faktora, posebno vrijedi da
dijeli svakog od tih faktora, posebno vrijedi da  dijeli razliku tih brojeva:
dijeli razliku tih brojeva: 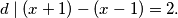 Dakle,
Dakle, 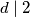 , pa su jedine mogućnosti za
, pa su jedine mogućnosti za 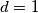 i
i 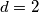 . Ovo u nekim zadatcima može voditi na dva slučaja. U prvom, kao što smo imali u prošlom zadatku, faktori
. Ovo u nekim zadatcima može voditi na dva slučaja. U prvom, kao što smo imali u prošlom zadatku, faktori  i
i  imaju zajedničku mjeru
imaju zajedničku mjeru  , dakle relativno su prosti i umnožak im je
, dakle relativno su prosti i umnožak im je  . U drugom slučaju,
. U drugom slučaju,  i
i  imaju zajedničku mjeru
imaju zajedničku mjeru  . Posebno, oba su parna, pa su zato
. Posebno, oba su parna, pa su zato 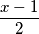 i
i 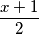 relativno prosti brojevi čiji je umnožak jednak
relativno prosti brojevi čiji je umnožak jednak 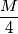 . U oba slučaja na lijevoj strani jednakosti sada imamo umnožak relativno prostih brojeva.
. U oba slučaja na lijevoj strani jednakosti sada imamo umnožak relativno prostih brojeva. na proste faktore kao u prošlom zadatku, sada možemo zaključiti da je svaka potencija prostog broja nužno sadržana u točno jednom od faktora s lijeve strane. Postoje zadatci i u kojima je
na proste faktore kao u prošlom zadatku, sada možemo zaključiti da je svaka potencija prostog broja nužno sadržana u točno jednom od faktora s lijeve strane. Postoje zadatci i u kojima je  još manje poznatog oblika, recimo, samo znamo da je potpun kvadrat ili potpun kub. Tada koristimo tvrdnju: ako je umnožak relativno prostih brojeva
još manje poznatog oblika, recimo, samo znamo da je potpun kvadrat ili potpun kub. Tada koristimo tvrdnju: ako je umnožak relativno prostih brojeva  i
i  potpun kvadrat / kub, tada je svaki od brojeva
potpun kvadrat / kub, tada je svaki od brojeva  i
i  potpun kvadrat / kub. Tvrdnja naravno vrijedi i za više potencije.
potpun kvadrat / kub. Tvrdnja naravno vrijedi i za više potencije.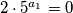 ), a ponekad možemo dobiti jedan novi mali zadatak kojem pristupamo kao i originalnom zadatku: modularna aritmetika, faktorizacija, eventualno traženje mjere i sl.
), a ponekad možemo dobiti jedan novi mali zadatak kojem pristupamo kao i originalnom zadatku: modularna aritmetika, faktorizacija, eventualno traženje mjere i sl.