Vrijeme: 01:54
Kolinearnost i kopunktalnost - Primjer 1
Primjer: Zadan je tetivan četverokut  . Pravci
. Pravci  i
i  sijeku se u točki
sijeku se u točki  , a pravci
, a pravci  i
i  u točki
u točki  . Krugovi opisani oko trokuta
. Krugovi opisani oko trokuta 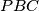 i
i 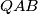 imaju zajedničku tetivu
imaju zajedničku tetivu 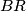 . Dokaži da su točke
. Dokaži da su točke 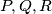 kolinearne.
kolinearne.
Rješenje:
Postoje različiti alati dokazivanja kolinearnosti, ali možda najosnovniji je uz pomoć računanja kuteva. Kolinearnost možemo dokazati tako što pokažemo da je zbroj onih kuteva koji bi bili suplementni ukoliko kolinearnost vrijedi jednak baš 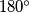 . U našem primjeru dovoljno je dokazati
. U našem primjeru dovoljno je dokazati 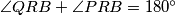 Primijetimo da je
Primijetimo da je 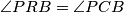 , te da je
, te da je 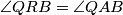 iz tetivnosti četverokuta
iz tetivnosti četverokuta 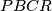 i
i 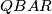 redom. Kako je i četverokut
redom. Kako je i četverokut  tetivan vrijedi
tetivan vrijedi 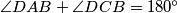 , odnosno
, odnosno 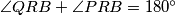 , odakle slijedi kolinearnost točaka
, odakle slijedi kolinearnost točaka  .
.
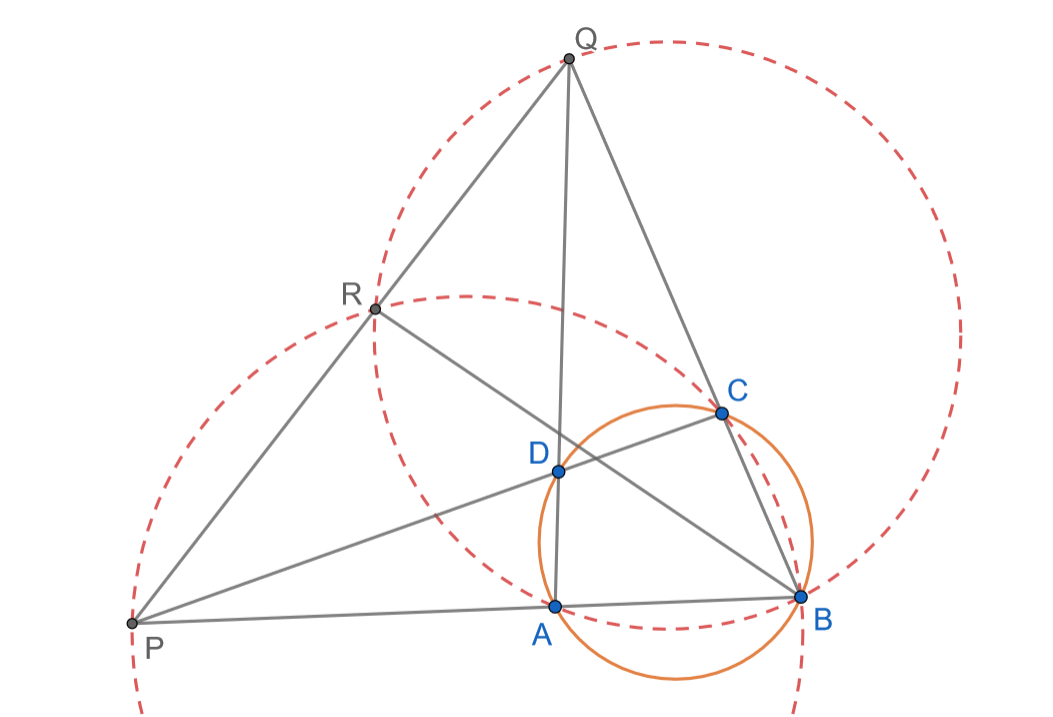
Za one koji žele malo više istražiti ovu konfiguraciju preporučam da istražite Mikelov teorem
Upišite  za nastavak.
za nastavak.
