Primjer: Zadan je trapez  u kojem je
u kojem je 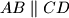 . Neka su
. Neka su  i
i  polovišta stranica
polovišta stranica  i
i  , redom. Dokaži da su pravci
, redom. Dokaži da su pravci 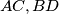 i
i  kopunktalni, odnosno da se sijeku u jednoj točki.
kopunktalni, odnosno da se sijeku u jednoj točki.
Rješenje:
Označimo sa  sjecište dijagonala trapeza
sjecište dijagonala trapeza  . Na ovom primjeru dobro vidimo dualnost između dokazivanja kolinearnosti i kopunktalnosti. Naime, dokazivanje da su pravci
. Na ovom primjeru dobro vidimo dualnost između dokazivanja kolinearnosti i kopunktalnosti. Naime, dokazivanje da su pravci 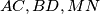 kopunktalni ekvivalentno je sa dokazivanjem da su točke
kopunktalni ekvivalentno je sa dokazivanjem da su točke 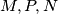 kolinearne gdje smo
kolinearne gdje smo  definirali kao sjecište
definirali kao sjecište  i
i  . Probajmo prvo zadatak riješiti na ovaj način.
. Probajmo prvo zadatak riješiti na ovaj način.
Malena modifikacija ideje iz prvog primjera daje nam da nam je potrebno i dovoljno pokazati da vrijedi 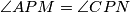 što se na prvi pogled ne čini trivijalno. Naime, ukoliko se malo poigrate sa zadatkom vidjet ćete da ove kuteve ne možemo izraziti preko unutarnjih kuteva trapeza, kao što ni u proizvoljnom trokutu ne možemo izraziti kut pod kojim ide težišnica preko unutarnjih kuteva trokuta. Na ovom mjestu lako je pomisliti da se zadatak ne može riješiti na ovaj način. Ipak, pokušajmo još malo razmisliti kako možemo povezati kuteve
što se na prvi pogled ne čini trivijalno. Naime, ukoliko se malo poigrate sa zadatkom vidjet ćete da ove kuteve ne možemo izraziti preko unutarnjih kuteva trapeza, kao što ni u proizvoljnom trokutu ne možemo izraziti kut pod kojim ide težišnica preko unutarnjih kuteva trokuta. Na ovom mjestu lako je pomisliti da se zadatak ne može riješiti na ovaj način. Ipak, pokušajmo još malo razmisliti kako možemo povezati kuteve  i
i 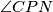 . Kut
. Kut  je kut pod kojim ide težišnica
je kut pod kojim ide težišnica 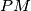 u trokutu
u trokutu 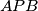 , a kut
, a kut 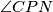 je kut pod kojim ide težišnica
je kut pod kojim ide težišnica 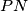 u trokutu
u trokutu 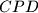 . Znamo li nešto za ta dva trokuta? Pa znamo! Oni su slični jer je
. Znamo li nešto za ta dva trokuta? Pa znamo! Oni su slični jer je  trapez. O sličnosti možemo razmišljati kao o transformaciji koja odgovarajuću sliku uveća ili umanji, ali zadržava omjere i kuteve. To znači da će odgovarajući elementi u sličnim trokutima ići pod istim kutevima, odnosno odgovarajuće težišnice će ići pod istim kutevima. Sada vidimo da imamo upravo tu situaciju. Trokuti
trapez. O sličnosti možemo razmišljati kao o transformaciji koja odgovarajuću sliku uveća ili umanji, ali zadržava omjere i kuteve. To znači da će odgovarajući elementi u sličnim trokutima ići pod istim kutevima, odnosno odgovarajuće težišnice će ići pod istim kutevima. Sada vidimo da imamo upravo tu situaciju. Trokuti 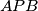 i
i 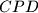 imaju isti kut u vrhu
imaju isti kut u vrhu  i
i 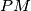 i
i 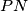 su baš odgovarajuće težišnice u ovim trokutima pa moraju ići pod istim kutem. Odavdje je
su baš odgovarajuće težišnice u ovim trokutima pa moraju ići pod istim kutem. Odavdje je 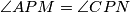 što smo i željeli dokazati. Za kraj, naglasio bih da zapamtite ovu ideju da u sličnim trokutima težišnice (i općenito odgovarajući elementi) idu pod istim kutem. U raznim zadacima, ne samo onim vezanim za kolinearnost i kopunktalnost ona se može pokazati veoma korisnom da povežemo naizgled nepovezane kuteve.
što smo i željeli dokazati. Za kraj, naglasio bih da zapamtite ovu ideju da u sličnim trokutima težišnice (i općenito odgovarajući elementi) idu pod istim kutem. U raznim zadacima, ne samo onim vezanim za kolinearnost i kopunktalnost ona se može pokazati veoma korisnom da povežemo naizgled nepovezane kuteve.
Zadatak se mogao riješiti i na jedan malo drugačiji način koji nam je standardan alat za dokazivanje kopunktalnosti. Naime, dovoljno je dokazati da pravci  i
i  sijeku dužinu
sijeku dužinu  u istom omjeru, tj. da ako sa
u istom omjeru, tj. da ako sa  kao i do sada označimo sjecište
kao i do sada označimo sjecište  i
i  , a sa
, a sa 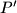 sjecište
sjecište  i
i  dovoljno je pokazati
dovoljno je pokazati 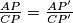 jer će odavdje slijediti da
jer će odavdje slijediti da  i
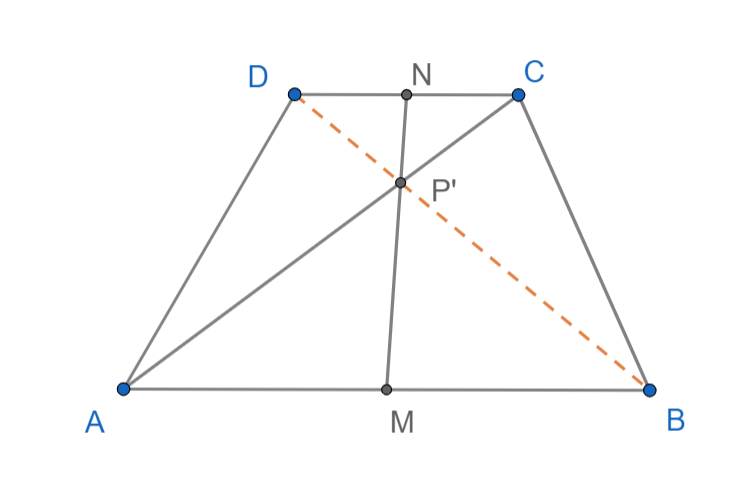
i 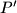 moraju biti ista točka. Vjerujem da vam je to jasno na intuitivnom nivou, a oni maksimalno pedantni se mogu uvjeriti u to dosta jednostavnim raspisivanjem, samo zapišite
moraju biti ista točka. Vjerujem da vam je to jasno na intuitivnom nivou, a oni maksimalno pedantni se mogu uvjeriti u to dosta jednostavnim raspisivanjem, samo zapišite 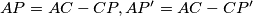 i pogledajte što postaje jednakost omjera.
i pogledajte što postaje jednakost omjera.
Gledajući prvu sliku i koristeći već spomenutu sličnost trokutova 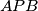 i
i 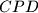 (ili Talesov teorem) imamo da vrijedi
(ili Talesov teorem) imamo da vrijedi 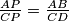 . S druge strane ako gledamo drugu sliku iz istih razloga, zbog
. S druge strane ako gledamo drugu sliku iz istih razloga, zbog 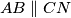 , su trokuti
, su trokuti 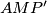 i
i 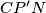 slični. Odavdje imamo da vrijedi
slični. Odavdje imamo da vrijedi 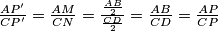 što smo i htjeli dobiti.
što smo i htjeli dobiti.
Za kraj ovog primjera naglasio bih da je jako važno da zapamtite ovu ideju za dokazivanje konkurentnosti, dokazivanje da 2 pravca sijeku treći u istom omjeru. Može biti jako korisna i kod težih zadataka. U ovom konkretnom slučaju mogli smo bez problema odabrati i da dokazujemo da  i
i  sijeku
sijeku  u istom omjeru ili da
u istom omjeru ili da  i
i  sijeku
sijeku  u istom omjeru. Ipak, ponekad treba biti oprezan sa tim što ćemo točno od toga dokazivati jer jedna opcija može biti mnogo lakša od drugih.
u istom omjeru. Ipak, ponekad treba biti oprezan sa tim što ćemo točno od toga dokazivati jer jedna opcija može biti mnogo lakša od drugih.
Upišite  za nastavak.
za nastavak.
\textbf{Primjer}: Zadan je trapez $ABCD$ u kojem je $AB \parallel CD$. Neka su $M$ i $N$ polovišta stranica $AB$ i $CD$, redom. Dokaži da su pravci $AC,BD$ i $MN$ kopunktalni, odnosno da se sijeku u jednoj točki. \\
\\
\textbf{Rješenje}: \\
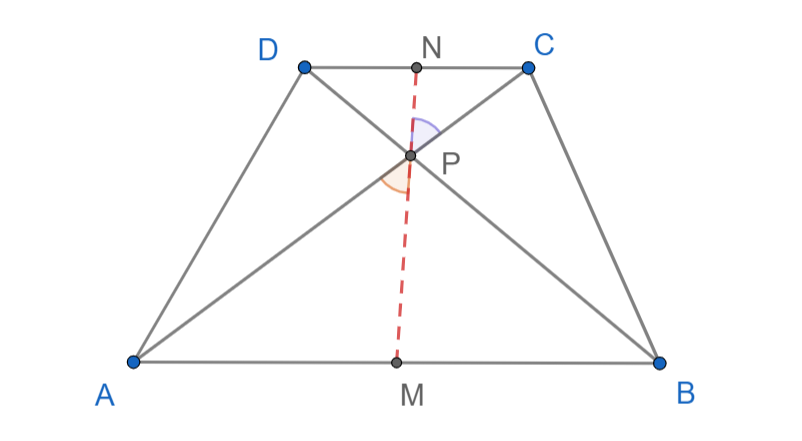
Označimo sa $P$ sjecište dijagonala trapeza $ABCD$. Na ovom primjeru dobro vidimo dualnost između dokazivanja kolinearnosti i kopunktalnosti. Naime, dokazivanje da su pravci $AC,BD,MN$ kopunktalni ekvivalentno je sa dokazivanjem da su točke $M,P,N$ kolinearne gdje smo $P$ definirali kao sjecište $AC$ i $BD$. Probajmo prvo zadatak riješiti na ovaj način.
\begin{center}
\includegraphics{trapez_3.png}
\end{center}
Malena modifikacija ideje iz prvog primjera daje nam da nam je potrebno i dovoljno pokazati da vrijedi $\angle APM=\angle CPN$ što se na prvi pogled ne čini trivijalno. Naime, ukoliko se malo poigrate sa zadatkom vidjet ćete da ove kuteve ne možemo izraziti preko unutarnjih kuteva trapeza, kao što ni u proizvoljnom trokutu ne možemo izraziti kut pod kojim ide težišnica preko unutarnjih kuteva trokuta. Na ovom mjestu lako je pomisliti da se zadatak ne može riješiti na ovaj način. Ipak, pokušajmo još malo razmisliti kako možemo povezati kuteve $\angle APM$ i $\angle CPN$. Kut $\angle APM$ je kut pod kojim ide težišnica $PM$ u trokutu $APB$, a kut $\angle CPN$ je kut pod kojim ide težišnica $PN$ u trokutu $CPD$. Znamo li nešto za ta dva trokuta? Pa znamo! Oni su slični jer je $ABCD$ trapez. O sličnosti možemo razmišljati kao o transformaciji koja odgovarajuću sliku uveća ili umanji, ali zadržava omjere i kuteve. To znači da će odgovarajući elementi u sličnim trokutima ići pod istim kutevima, odnosno odgovarajuće težišnice će ići pod istim kutevima. Sada vidimo da imamo upravo tu situaciju. Trokuti $APB$ i $CPD$ imaju isti kut u vrhu $P$ i $PM$ i $PN$ su baš odgovarajuće težišnice u ovim trokutima pa moraju ići pod istim kutem. Odavdje je $\angle APM=\angle CPN$ što smo i željeli dokazati. Za kraj, naglasio bih da zapamtite ovu ideju da u sličnim trokutima težišnice (i općenito odgovarajući elementi) idu pod istim kutem. U raznim zadacima, ne samo onim vezanim za kolinearnost i kopunktalnost ona se može pokazati veoma korisnom da povežemo naizgled nepovezane kuteve. \\
Zadatak se mogao riješiti i na jedan malo drugačiji način koji nam je standardan alat za dokazivanje kopunktalnosti. Naime, dovoljno je dokazati da pravci $BD$ i $MN$ sijeku dužinu $AC$ u istom omjeru, tj. da ako sa $P$ kao i do sada označimo sjecište $AC$ i $BD$, a sa $P'$ sjecište $MN$ i $AC$ dovoljno je pokazati $\frac{AP}{CP}=\frac{AP'}{CP'}$ jer će odavdje slijediti da $P$ i $P'$ moraju biti ista točka. Vjerujem da vam je to jasno na intuitivnom nivou, a oni maksimalno pedantni se mogu uvjeriti u to dosta jednostavnim raspisivanjem, samo zapišite $AP=AC-CP,AP'=AC-CP'$ i pogledajte što postaje jednakost omjera.
\begin{center}
\includegraphics{trapez_2.png}
\end{center}
Gledajući prvu sliku i koristeći već spomenutu sličnost trokutova $APB$ i $CPD$ (ili Talesov teorem) imamo da vrijedi $\frac{AP}{CP}=\frac{AB}{CD}$. S druge strane ako gledamo drugu sliku iz istih razloga, zbog $AB \parallel CN$, su trokuti $AMP'$ i $CP'N$ slični. Odavdje imamo da vrijedi $\frac{AP'}{CP'}=\frac{AM}{CN}=\frac{\frac{AB}{2}}{\frac{CD}{2}}=\frac{AB}{CD}=\frac{AP}{CP}$ što smo i htjeli dobiti. \\
Za kraj ovog primjera naglasio bih da je jako važno da zapamtite ovu ideju za dokazivanje konkurentnosti, dokazivanje da 2 pravca sijeku treći u istom omjeru. Može biti jako korisna i kod težih zadataka. U ovom konkretnom slučaju mogli smo bez problema odabrati i da dokazujemo da $BD$ i $AC$ sijeku $MN$ u istom omjeru ili da $MN$ i $AC$ sijeku $BD$ u istom omjeru. Ipak, ponekad treba biti oprezan sa tim što ćemo točno od toga dokazivati jer jedna opcija može biti mnogo lakša od drugih. \\
\\
Upišite $1$ za nastavak.
 u kojem je
u kojem je 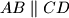 . Neka su
. Neka su  i
i  polovišta stranica
polovišta stranica  i
i  , redom. Dokaži da su pravci
, redom. Dokaži da su pravci 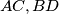 i
i  kopunktalni, odnosno da se sijeku u jednoj točki.
kopunktalni, odnosno da se sijeku u jednoj točki.  sjecište dijagonala trapeza
sjecište dijagonala trapeza  . Na ovom primjeru dobro vidimo dualnost između dokazivanja kolinearnosti i kopunktalnosti. Naime, dokazivanje da su pravci
. Na ovom primjeru dobro vidimo dualnost između dokazivanja kolinearnosti i kopunktalnosti. Naime, dokazivanje da su pravci 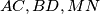 kopunktalni ekvivalentno je sa dokazivanjem da su točke
kopunktalni ekvivalentno je sa dokazivanjem da su točke 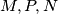 kolinearne gdje smo
kolinearne gdje smo  definirali kao sjecište
definirali kao sjecište  i
i  . Probajmo prvo zadatak riješiti na ovaj način.
. Probajmo prvo zadatak riješiti na ovaj način. 
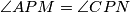 što se na prvi pogled ne čini trivijalno. Naime, ukoliko se malo poigrate sa zadatkom vidjet ćete da ove kuteve ne možemo izraziti preko unutarnjih kuteva trapeza, kao što ni u proizvoljnom trokutu ne možemo izraziti kut pod kojim ide težišnica preko unutarnjih kuteva trokuta. Na ovom mjestu lako je pomisliti da se zadatak ne može riješiti na ovaj način. Ipak, pokušajmo još malo razmisliti kako možemo povezati kuteve
što se na prvi pogled ne čini trivijalno. Naime, ukoliko se malo poigrate sa zadatkom vidjet ćete da ove kuteve ne možemo izraziti preko unutarnjih kuteva trapeza, kao što ni u proizvoljnom trokutu ne možemo izraziti kut pod kojim ide težišnica preko unutarnjih kuteva trokuta. Na ovom mjestu lako je pomisliti da se zadatak ne može riješiti na ovaj način. Ipak, pokušajmo još malo razmisliti kako možemo povezati kuteve  i
i 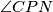 . Kut
. Kut  je kut pod kojim ide težišnica
je kut pod kojim ide težišnica 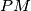 u trokutu
u trokutu 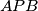 , a kut
, a kut 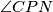 je kut pod kojim ide težišnica
je kut pod kojim ide težišnica 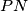 u trokutu
u trokutu 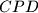 . Znamo li nešto za ta dva trokuta? Pa znamo! Oni su slični jer je
. Znamo li nešto za ta dva trokuta? Pa znamo! Oni su slični jer je  trapez. O sličnosti možemo razmišljati kao o transformaciji koja odgovarajuću sliku uveća ili umanji, ali zadržava omjere i kuteve. To znači da će odgovarajući elementi u sličnim trokutima ići pod istim kutevima, odnosno odgovarajuće težišnice će ići pod istim kutevima. Sada vidimo da imamo upravo tu situaciju. Trokuti
trapez. O sličnosti možemo razmišljati kao o transformaciji koja odgovarajuću sliku uveća ili umanji, ali zadržava omjere i kuteve. To znači da će odgovarajući elementi u sličnim trokutima ići pod istim kutevima, odnosno odgovarajuće težišnice će ići pod istim kutevima. Sada vidimo da imamo upravo tu situaciju. Trokuti 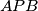 i
i 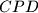 imaju isti kut u vrhu
imaju isti kut u vrhu  i
i 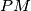 i
i 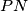 su baš odgovarajuće težišnice u ovim trokutima pa moraju ići pod istim kutem. Odavdje je
su baš odgovarajuće težišnice u ovim trokutima pa moraju ići pod istim kutem. Odavdje je 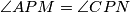 što smo i željeli dokazati. Za kraj, naglasio bih da zapamtite ovu ideju da u sličnim trokutima težišnice (i općenito odgovarajući elementi) idu pod istim kutem. U raznim zadacima, ne samo onim vezanim za kolinearnost i kopunktalnost ona se može pokazati veoma korisnom da povežemo naizgled nepovezane kuteve.
što smo i željeli dokazati. Za kraj, naglasio bih da zapamtite ovu ideju da u sličnim trokutima težišnice (i općenito odgovarajući elementi) idu pod istim kutem. U raznim zadacima, ne samo onim vezanim za kolinearnost i kopunktalnost ona se može pokazati veoma korisnom da povežemo naizgled nepovezane kuteve.  i
i  sijeku dužinu
sijeku dužinu  u istom omjeru, tj. da ako sa
u istom omjeru, tj. da ako sa  kao i do sada označimo sjecište
kao i do sada označimo sjecište  i
i  , a sa
, a sa 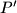 sjecište
sjecište  i
i  dovoljno je pokazati
dovoljno je pokazati 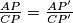 jer će odavdje slijediti da
jer će odavdje slijediti da  i
i 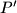 moraju biti ista točka. Vjerujem da vam je to jasno na intuitivnom nivou, a oni maksimalno pedantni se mogu uvjeriti u to dosta jednostavnim raspisivanjem, samo zapišite
moraju biti ista točka. Vjerujem da vam je to jasno na intuitivnom nivou, a oni maksimalno pedantni se mogu uvjeriti u to dosta jednostavnim raspisivanjem, samo zapišite 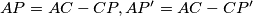 i pogledajte što postaje jednakost omjera.
i pogledajte što postaje jednakost omjera. 
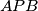 i
i 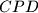 (ili Talesov teorem) imamo da vrijedi
(ili Talesov teorem) imamo da vrijedi 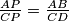 . S druge strane ako gledamo drugu sliku iz istih razloga, zbog
. S druge strane ako gledamo drugu sliku iz istih razloga, zbog 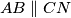 , su trokuti
, su trokuti 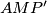 i
i 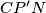 slični. Odavdje imamo da vrijedi
slični. Odavdje imamo da vrijedi 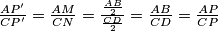 što smo i htjeli dobiti.
što smo i htjeli dobiti.  i
i  sijeku
sijeku  u istom omjeru ili da
u istom omjeru ili da  i
i  sijeku
sijeku  u istom omjeru. Ipak, ponekad treba biti oprezan sa tim što ćemo točno od toga dokazivati jer jedna opcija može biti mnogo lakša od drugih.
u istom omjeru. Ipak, ponekad treba biti oprezan sa tim što ćemo točno od toga dokazivati jer jedna opcija može biti mnogo lakša od drugih.  za nastavak.
za nastavak. 