Primjer: Neka je  kvadrat i
kvadrat i  kružnica sa središtem u točki
kružnica sa središtem u točki  koja prolazi točkama
koja prolazi točkama  i
i  , te neka je
, te neka je  točka na kružnici
točka na kružnici  unutar danog kvadrata. Tangenta na kružnicu
unutar danog kvadrata. Tangenta na kružnicu  u točki
u točki  siječe dužine
siječe dužine  i
i 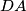 redom u točkama
redom u točkama  i
i  . Neka su
. Neka su  i
i  redom sjecišta pravaca
redom sjecišta pravaca  i
i 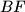 s dužinom
s dužinom  . Dokaži da pravci
. Dokaži da pravci 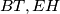 i
i 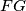 prolaze istom točkom.
prolaze istom točkom.
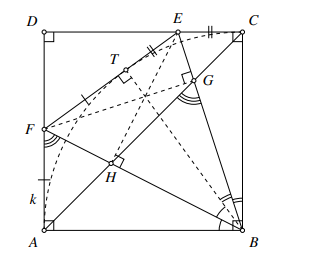
Rješenje: Ovaj zadatak je vjerojatno i poznat dijelu auditorija budući da se radi o zadatku sa HJMO 2018. Ipak, ovdje je jer nam dobro služi kao ilustracija da je nekad zgodan način za dokazati da se tri pravca sijeku u istoj točki da uočimo da se radi o nekoj karakterističnoj točki nekog trokuta na skici.
Točke 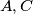 i
i  leže na kružnici
leže na kružnici  , a pravci
, a pravci 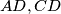 i
i  su tangente na k u tim točkama. Budući da je
su tangente na k u tim točkama. Budući da je  središte, a
središte, a  tangenta u
tangenta u  , vrijedi
, vrijedi 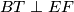 . Uočimo da su
. Uočimo da su  i
i  dirališta tangenti povučenih iz točke
dirališta tangenti povučenih iz točke  na kružnicu
na kružnicu  , pa vrijedi
, pa vrijedi 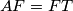 . Sada vidimo da su trokuti
. Sada vidimo da su trokuti 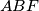 i
i 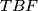 sukladni.Analogno je
sukladni.Analogno je 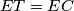 i trokuti
i trokuti 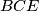 i
i 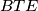 su sukladni.
su sukladni.
Označimo 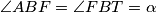 i
i 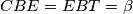 . Kako je
. Kako je 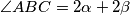 , slijedi
, slijedi 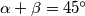 . Vrijedi
. Vrijedi 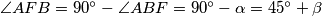 . Kako je
. Kako je 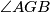 vanjski kut trokuta
vanjski kut trokuta 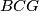 , vrijedi
, vrijedi 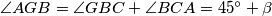 . Dakle,
. Dakle, 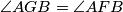 .
.
Kako su  i
i  s iste strane pravca
s iste strane pravca  , iz
, iz 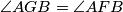 slijedi da je četverokut
slijedi da je četverokut 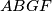 tetivan. Stoga je
tetivan. Stoga je 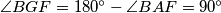 . Dakle, dokazali smo da je
. Dakle, dokazali smo da je 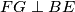 .
.
Analogno se pokazuje da je četverokut 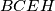 tetivan te
tetivan te 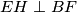 . Dokazali smo dakle da su dužine
. Dokazali smo dakle da su dužine 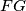 i
i 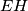 visine trokuta
visine trokuta 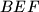 , a kako je i BT visina tog trokuta, zaključujemo da se pravci
, a kako je i BT visina tog trokuta, zaključujemo da se pravci 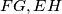 i
i 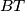 sijeku u jednoj točki, ortocentru tog trokuta.
sijeku u jednoj točki, ortocentru tog trokuta.
Upišite  za nastavak.
za nastavak.
\textbf{Primjer}: Neka je $ABCD$ kvadrat i $k$ kružnica sa središtem u točki $B$ koja prolazi
točkama $A$ i $C$, te neka je $T$ točka na kružnici $k$ unutar danog kvadrata. Tangenta na kružnicu $k$ u točki $T$ siječe dužine $CD$ i $DA$ redom u točkama $E$ i $F$. Neka su $G$ i $H$ redom sjecišta pravaca $BE$ i $BF$ s dužinom $AC$.
Dokaži da pravci $BT, EH$ i $FG$ prolaze istom točkom. \\
\\
\textbf{Rješenje}: Ovaj zadatak je vjerojatno i poznat dijelu auditorija budući da se radi o zadatku sa HJMO 2018. Ipak, ovdje je jer nam dobro služi kao ilustracija da je nekad zgodan način za dokazati da se tri pravca sijeku u istoj točki da uočimo da se radi o nekoj karakterističnoj točki nekog trokuta na skici.
\begin{center}
\includegraphics{hjmo.png} \end{center}
Točke $A, C$ i $T$ leže na kružnici $k$, a pravci $AD, CD$ i $EF$ su tangente na k u tim točkama. Budući da je $B$ središte, a $EF$ tangenta u $T$, vrijedi $BT \perp EF$. Uočimo da su $A$ i $T$ dirališta tangenti povučenih iz točke $F$ na kružnicu $k$, pa vrijedi $AF=FT$. Sada vidimo da su trokuti $ABF$ i $TBF$ sukladni.Analogno je $ET=EC$ i trokuti $BCE$ i $BTE$ su sukladni. \\
Označimo $\angle ABF = \angle FBT = \alpha$ i $CBE = EBT = \beta$. Kako je $\angle ABC = 2\alpha+ 2\beta$, slijedi $\alpha+\beta=45^{\circ}$. Vrijedi $\angle AFB = 90^{\circ}-\angle ABF = 90^{\circ} - \alpha= 45^{\circ} + \beta$. Kako je $\angle AGB$ vanjski kut trokuta $BCG$, vrijedi $\angle AGB = \angle GBC + \angle BCA = 45^{\circ} + \beta$. Dakle, $\angle AGB = \angle AFB$. \\
Kako su $F$ i $G$ s iste strane pravca $AB$, iz $\angle AGB = \angle AFB$ slijedi da je četverokut $ABGF$ tetivan. Stoga je $\angle BGF = 180^{\circ}-\angle BAF =
90^{\circ}$. Dakle, dokazali smo da je $FG \perp BE$. \\
Analogno se pokazuje da je četverokut $BCEH$ tetivan te $EH \perp BF$. Dokazali smo dakle da su dužine $FG$ i $EH$ visine trokuta $BEF$, a kako je i BT visina tog trokuta,
zaključujemo da se pravci $FG, EH$ i $BT$ sijeku u jednoj točki, ortocentru tog trokuta. \\
\\
Upišite $1$ za nastavak.
 kvadrat i
kvadrat i  kružnica sa središtem u točki
kružnica sa središtem u točki  koja prolazi točkama
koja prolazi točkama  i
i  , te neka je
, te neka je  točka na kružnici
točka na kružnici  unutar danog kvadrata. Tangenta na kružnicu
unutar danog kvadrata. Tangenta na kružnicu  u točki
u točki  siječe dužine
siječe dužine  i
i 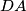 redom u točkama
redom u točkama  i
i  . Neka su
. Neka su  i
i  redom sjecišta pravaca
redom sjecišta pravaca  i
i 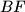 s dužinom
s dužinom  . Dokaži da pravci
. Dokaži da pravci 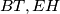 i
i 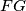 prolaze istom točkom.
prolaze istom točkom. 
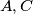 i
i  leže na kružnici
leže na kružnici  , a pravci
, a pravci 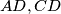 i
i  su tangente na k u tim točkama. Budući da je
su tangente na k u tim točkama. Budući da je  središte, a
središte, a  tangenta u
tangenta u  , vrijedi
, vrijedi 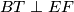 . Uočimo da su
. Uočimo da su  i
i  dirališta tangenti povučenih iz točke
dirališta tangenti povučenih iz točke  na kružnicu
na kružnicu  , pa vrijedi
, pa vrijedi 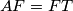 . Sada vidimo da su trokuti
. Sada vidimo da su trokuti 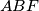 i
i 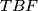 sukladni.Analogno je
sukladni.Analogno je 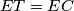 i trokuti
i trokuti 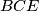 i
i 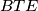 su sukladni.
su sukladni. 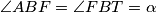 i
i 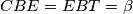 . Kako je
. Kako je 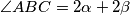 , slijedi
, slijedi 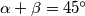 . Vrijedi
. Vrijedi 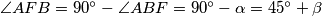 . Kako je
. Kako je 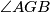 vanjski kut trokuta
vanjski kut trokuta 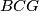 , vrijedi
, vrijedi 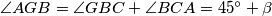 . Dakle,
. Dakle, 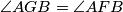 .
.  i
i  s iste strane pravca
s iste strane pravca  , iz
, iz 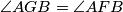 slijedi da je četverokut
slijedi da je četverokut 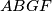 tetivan. Stoga je
tetivan. Stoga je 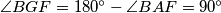 . Dakle, dokazali smo da je
. Dakle, dokazali smo da je 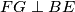 .
. 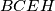 tetivan te
tetivan te 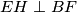 . Dokazali smo dakle da su dužine
. Dokazali smo dakle da su dužine 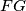 i
i 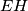 visine trokuta
visine trokuta 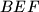 , a kako je i BT visina tog trokuta, zaključujemo da se pravci
, a kako je i BT visina tog trokuta, zaključujemo da se pravci 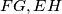 i
i 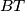 sijeku u jednoj točki, ortocentru tog trokuta.
sijeku u jednoj točki, ortocentru tog trokuta.  za nastavak.
za nastavak. 