Kolinearnost i kopunktalnost - Primjer 4
Primjer: Neka je  ortocentar šiljastokutnog trokuta
ortocentar šiljastokutnog trokuta  , a
, a  polovište stranice
polovište stranice  . Ako su
. Ako su  i
i  redom nožišta okomica iz točke
redom nožišta okomica iz točke  na simetralu unutarnjeg i vanjskog kuta kod vrha
na simetralu unutarnjeg i vanjskog kuta kod vrha  , dokazati da su točke
, dokazati da su točke 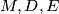 kolinearne.
kolinearne.
Rješenje: Slično kao što točka u kojoj se sijeku pravci može ispasti neka specijalna točka, tako i pravac na kom leže točke za koje trebamo dokazati da su kolinearne može biti neki specijalan pravac. U ovom zadatku nakon što tek nacrtamo skice točke 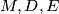 izgledaju solidno nepovezano i nije baš jasno kako bismo pristupili dokazivanju kolinearnosti. Fokusirajmo se na to što možemo odgnonetnuti o točkama
izgledaju solidno nepovezano i nije baš jasno kako bismo pristupili dokazivanju kolinearnosti. Fokusirajmo se na to što možemo odgnonetnuti o točkama  i
i  . Ove točke leže na kružnici nad promjerom
. Ove točke leže na kružnici nad promjerom 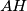 . Na toj kružnici leže i točke
. Na toj kružnici leže i točke 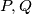 , nožišta visina trokuta
, nožišta visina trokuta  iz vrhova
iz vrhova  i
i  .
.
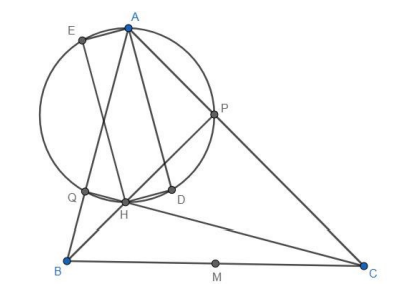
Kao što smo već rekli šesterokut 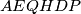 je tetivni. Neka je
je tetivni. Neka je  njegova opisana kružnica. Obodni kutevi
njegova opisana kružnica. Obodni kutevi  i
i 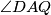 u kružnici
u kružnici  nad tetivama
nad tetivama 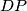 i
i 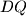 su jednaki jer je
su jednaki jer je  simetrala kuta, pa su i odgovarajuće tetive jednake, tj.
simetrala kuta, pa su i odgovarajuće tetive jednake, tj. 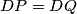 . Slično, zbog
. Slično, zbog 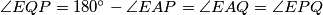 vrijedi
vrijedi 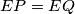 . Ovdje smo koristili da je zbroj suprotnih kuteva kod tetivnog četverokuta
. Ovdje smo koristili da je zbroj suprotnih kuteva kod tetivnog četverokuta 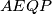 jednak
jednak 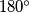 i da je
i da je  simetrala vanjskog kuta. Dakle pravac
simetrala vanjskog kuta. Dakle pravac  zaista jest simetrala dužine
zaista jest simetrala dužine  . Ostaje još dokazati da je
. Ostaje još dokazati da je  na simetrali dužine
na simetrali dužine  .
.
Točka  je polovište hipotenuze
je polovište hipotenuze  u pravokutnim trokutima
u pravokutnim trokutima 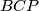 i
i  , pa je
, pa je  i središte kružnica opisanih oko tih trokutova, odakle je
i središte kružnica opisanih oko tih trokutova, odakle je 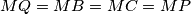 dakle
dakle  pripada simetrali dužine
pripada simetrali dužine  odakle slijedi da su
odakle slijedi da su 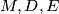 kolinearne.
kolinearne.
Upišite  za nastavak.
za nastavak.
