Primjer: Skakavac se nalazi gornjem lijevom kutu 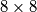 ploče podijeljenu na jedinične kvadratiće i želi stići do donjeg desnog kuta ploče, tako da posjeti svako polje ploče točno jednom. Da li skakavac može ostvariti svoj cilj?
ploče podijeljenu na jedinične kvadratiće i želi stići do donjeg desnog kuta ploče, tako da posjeti svako polje ploče točno jednom. Da li skakavac može ostvariti svoj cilj?
Rješenje:
Najčešće bojanje ploče je bojanje na šahovski način, tj. u crno-bijele boje gdje su susjedna polja ploče različito obojena. Primjećujemo da stojeći na bijelom polju možemo se kretati samo na crno polje i obrnuto. Početno polje može biti crno ili bijelo, pa bez gubitka općenitosti recimo da je gornje lijevo polje bijelo. Ostaje nam 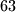 polja za kretanje, što znači da skakavac ima još
polja za kretanje, što znači da skakavac ima još 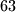 poteza. Jer počinje na bijelom polju, nakon prvog poteza skakavac je na crnom polju. Nakon drugog poteza je na bijelom polju, a nakon trećeg na crnom polju. Vidimo da je nakon svakog neparnog poteza na crnom polju, a nakon svakog parnog poteza na bijelom polju. Ova činjenica je naša invarijanta. Nakon što skakavac napravi
poteza. Jer počinje na bijelom polju, nakon prvog poteza skakavac je na crnom polju. Nakon drugog poteza je na bijelom polju, a nakon trećeg na crnom polju. Vidimo da je nakon svakog neparnog poteza na crnom polju, a nakon svakog parnog poteza na bijelom polju. Ova činjenica je naša invarijanta. Nakon što skakavac napravi 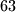 poteza, pošto je to neparan broj, završiti će na crnom polju. Međutim, suprotni kutovi (gornji lijevi i donji desni) imaju istu boju, u našem slučaju bijelu, pa ne može skakavac u zadnjem potezu završiti u donjem desnom kutu.
poteza, pošto je to neparan broj, završiti će na crnom polju. Međutim, suprotni kutovi (gornji lijevi i donji desni) imaju istu boju, u našem slučaju bijelu, pa ne može skakavac u zadnjem potezu završiti u donjem desnom kutu.
Upišite  za nastavak.
za nastavak.
\textbf{Primjer}: Skakavac se nalazi gornjem lijevom kutu $8 \times 8$ ploče podijeljenu na jedinične kvadratiće i želi stići do donjeg desnog kuta ploče, tako da posjeti svako polje ploče točno jednom. Da li skakavac može ostvariti svoj cilj?
\textbf{Rješenje:}
Najčešće bojanje ploče je bojanje na šahovski način, tj. u crno-bijele boje gdje su susjedna polja ploče različito obojena. Primjećujemo da stojeći na bijelom polju možemo se kretati samo na crno polje i obrnuto. Početno polje može biti crno ili bijelo, pa bez gubitka općenitosti recimo da je gornje lijevo polje bijelo. Ostaje nam $63$ polja za kretanje, što znači da skakavac ima još $63$ poteza. Jer počinje na bijelom polju, nakon prvog poteza skakavac je na crnom polju. Nakon drugog poteza je na bijelom polju, a nakon trećeg na crnom polju. Vidimo da je nakon svakog neparnog poteza na crnom polju, a nakon svakog parnog poteza na bijelom polju. Ova činjenica je naša invarijanta. Nakon što skakavac napravi $63$ poteza, pošto je to neparan broj, završiti će na crnom polju. Međutim, suprotni kutovi (gornji lijevi i donji desni) imaju istu boju, u našem slučaju bijelu, pa ne može skakavac u zadnjem potezu završiti u donjem desnom kutu.
\begin{center}
\includegraphics{sahovskislika.JPG}
\end{center}
Upišite $1$ za nastavak.
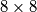 ploče podijeljenu na jedinične kvadratiće i želi stići do donjeg desnog kuta ploče, tako da posjeti svako polje ploče točno jednom. Da li skakavac može ostvariti svoj cilj?
ploče podijeljenu na jedinične kvadratiće i želi stići do donjeg desnog kuta ploče, tako da posjeti svako polje ploče točno jednom. Da li skakavac može ostvariti svoj cilj?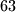 polja za kretanje, što znači da skakavac ima još
polja za kretanje, što znači da skakavac ima još 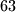 poteza. Jer počinje na bijelom polju, nakon prvog poteza skakavac je na crnom polju. Nakon drugog poteza je na bijelom polju, a nakon trećeg na crnom polju. Vidimo da je nakon svakog neparnog poteza na crnom polju, a nakon svakog parnog poteza na bijelom polju. Ova činjenica je naša invarijanta. Nakon što skakavac napravi
poteza. Jer počinje na bijelom polju, nakon prvog poteza skakavac je na crnom polju. Nakon drugog poteza je na bijelom polju, a nakon trećeg na crnom polju. Vidimo da je nakon svakog neparnog poteza na crnom polju, a nakon svakog parnog poteza na bijelom polju. Ova činjenica je naša invarijanta. Nakon što skakavac napravi 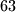 poteza, pošto je to neparan broj, završiti će na crnom polju. Međutim, suprotni kutovi (gornji lijevi i donji desni) imaju istu boju, u našem slučaju bijelu, pa ne može skakavac u zadnjem potezu završiti u donjem desnom kutu.
poteza, pošto je to neparan broj, završiti će na crnom polju. Međutim, suprotni kutovi (gornji lijevi i donji desni) imaju istu boju, u našem slučaju bijelu, pa ne može skakavac u zadnjem potezu završiti u donjem desnom kutu.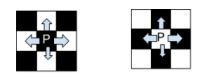
 za nastavak.
za nastavak. 