MetaMath '23

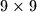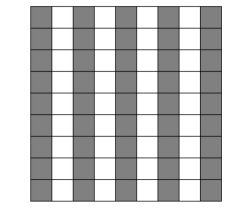
\textbf{Primjer}: U svakom polju ploče $9 \times 9$ sjedi po jedna žaba. U nekom trenutku svaka žaba skače dijagonalno u neko od četiri polja koja imaju zajednički vrh s poljem u kojem se prvotno nalazila (može se dogoditi da se više žaba nađe u jednom polju). Odrediti koliko najmanje polja ostane prazno nakon takvog skoka. \textbf{Rješenje}: Nekada bojanje po retcima i stupcima može biti jako korisno (tipa bojanje svakog drugog ili trećeg ili četvrtog itd. stupca ili retka), pa uvijek treba takvo bojanje probati. Obojimo stupce ploče na način prikazan na slici. Na taj način dobijemo 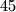$45$ sivih i 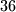$36$ bijelih polja. Pri svakom skoku, žaba mijenja boju polja na kojem se nalazi. Stoga će barem $9$ sivih polja ostati prazno nakon svih skokova. Ako bismo sad pronašli konstrukciju skokova koja daje upravo $9$ praznih polja, zadatak bi bio gotov. Opisat ćemo jednu moguću konstrukciju. U donjoj lijevoj podtabli visine $2$, širine $8$ žabe dijagonalno zamjene mjesta, te isto tako u desnoj gornjoj podtabli visine $6$, širine $2$. U nastalom "L" obliku u donjem desnom kutu dvije žabe koje mogu zamijeniti mjesto zamjene, a polje skroz dolje desno i ono dva mjesta iznad ostanu bez žaba (žabe koje su bile tamo skoče bilo gdje). 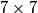Sad smo reducirali tablu na $7 \times 7$ podtablu. 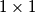Postupak ponavljamo $4$ puta do $1 \times 1$ podtable, tj. gornjeg lijevog kvadratića koji ostaje prazan, te nam je ostalo još 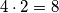$4 \cdot 2 = 8$ praznih polja tokom postupka. \begin{center}      \includegraphics{Traka.JPG}  \end{center} \\ Upišite $1$ za nastavak.