MetaMath '23

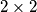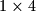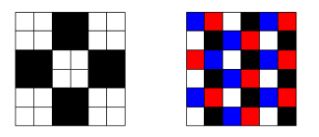
\textbf{Primjer}: Pravokutni pod prekriven je pločama $2 \times 2$ i $1 \times 4$. Jedna se ploča razbila, no dostupna nam je ploča drugog oblika. Dokazati da se pod ne može prekriti prerazmještajem ovih ploča. \textbf{Rješenje:} Nekada ova prethodna "fina" bojanja ne prolaze, pa moramo nekada preći na neka nestandardnija i biti kreativni. Ono što je bitno da u većini slučajeva nam je bitno da to naše bojanje mora biti simetrično, jer ne želimo da postavljanje nekog oblika zavisi od toga u kom smo ga dijelu ploče postavili. Za ovaj zadatak se ispostavlja da je ovo bojanje korisno: \begin{center} \includegraphics{Tackasti.JPG} \end{center} Svaka figura formata 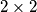$2 \times 2$ pokriva točno jedno crno polje, dok figure formata 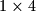$1 \times 4$ pokrivaju $0$ ili $2$ crna polja. Kada zamijenimo figuru jednog formata figurom drugog formata, novi skup figura ne može pokriti isti broj crnih polja (jer mijenjamo figuru koja pokriva jedno polje figurom koja pokriva $0$ ili $2$, ili obratno). Zaključujemo da novim skupom figura ne možemo popločati ploču. Imaju još razne vrsta bojanja i nećemo sada u primjerima proći kroz sve moguće, nego ćete "pokupiti" još neke ideje za bojanje kroz izradu ovih lanaca. Neki od još poznatih bojanja su: \begin{center} \includegraphics{primjeriboj.JPG} \end{center} \begin{center} \includegraphics{tri.JPG} \end{center} Upišite $1$ za nastavak.