MetaMath '23

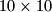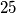\textbf{Zadatak 5}: Na ploču $10 \times 10$ postavljeno je $50$ žetona tako da nikoja dva nisu na istom polju. Pritom $25$ žetona zauzima donju lijevu četvrtinu ploče, a preostalih 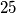$25$ gornju desnu četvrtinu. Neka su 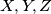$X, Y, Z$ redom tri uzastopna polja (horizontalno, vertikalno ili dijagonalno). Ako se dva žetona nalaze na poljima $X$ i $Y$ i ako je polje $Z$ slobodno, žeton s polja $X$ može se premjestiti na polje $Z$, preskočivši žeton na polju $Y$. Može li se, konačnim nizom takvih poteza, premjestiti svih $50$ žetona na donju polovicu ploče? \textit{Molim vas da uploadate sliku kao rješenje ako ste u mogućnosti.}