Da ne bude da ga nismo spomenuli, evo dva na brzinu odabrana zadatka iz Engelovih Strategija rješavanja problema, takozvane ,,Biblije za natjecateljsku matematiku''. Zadaci su namijenjeni prvenstveno iskusnijim natjecateljima, ali možete se slobodno okušati!
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Neka su nizovi brojeva  ,
,  ,
,  ,
,  i
i 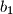 ,
, 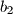 ,
,  ,
, 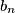 dvije permutacije niza brojeva
dvije permutacije niza brojeva  ,
,  ,
,  ,
, 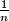 takve da vrijedi
takve da vrijedi  .
.
Dokažite da vrijedi  za sve
za sve  između
između  i
i  .
.
Da ne bude da ga nismo spomenuli, evo dva na brzinu odabrana zadatka iz Engelovih Strategija rješavanja problema, takozvane ,,Biblije za natjecateljsku matematiku''. Zadaci su namijenjeni prvenstveno iskusnijim natjecateljima, ali možete se slobodno okušati!
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Neka su nizovi brojeva $a_1$, $a_2$, $\ldots$, $a_n$ i $b_1$, $b_2$, $\ldots$, $b_n$ dvije permutacije niza brojeva $1$, $\frac{1}{2}$, $\ldots$, $\frac{1}{n}$ takve da vrijedi $a_1 + b_1 \ge a_2 + b_2 \ge \dotsb \ge a_n + b_n$.
Dokažite da vrijedi $a_k + b_k \le \frac{4}{k}$ za sve $k$ između $1$ i $n$.
 ,
,  ,
,  ,
,  i
i 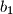 ,
, 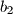 ,
,  ,
, 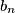 dvije permutacije niza brojeva
dvije permutacije niza brojeva  ,
,  ,
,  ,
, 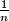 takve da vrijedi
takve da vrijedi  .
. za sve
za sve  između
između  i
i  .
. 