U prvom tjednu ovogodišnjeg MetaMath tečaja bavit ćemo se nejednakostima.
Kao što znakom  uspostavljamo jednakost nekih dviju vrijednosti, znakovima
uspostavljamo jednakost nekih dviju vrijednosti, znakovima  ,
,  ,
,  ,
,  uspostavlja se nejednakost između dviju vrijednosti. Kao što razlikujemo pojam jednadžbe od pojma jednakosti, razlikujemo i nejednadžbu od nejednakosti.
uspostavlja se nejednakost između dviju vrijednosti. Kao što razlikujemo pojam jednadžbe od pojma jednakosti, razlikujemo i nejednadžbu od nejednakosti.
Primjer 1
Odredite sve 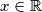 za koje je
za koje je  .
.
Rješenje
Dodavanjem jedinice s obje strane dobivamo da je početna nejednakost ekvivalentna s  . Ovo je ekvivalentno s
. Ovo je ekvivalentno s  . Rješenja nejednadžbe su svi
. Rješenja nejednadžbe su svi ![x\in [-2,0]](/media/m/f/e/0/fe04198a93ce1539a466feb3a24877ee.png) .
.
Kao rješenje upišite najmanji broj koji je rješenje ove nejednadžbe.
U prvom tjednu ovogodišnjeg MetaMath tečaja bavit ćemo se \textbf{nejednakostima}.
Kao što znakom $=$ uspostavljamo jednakost nekih dviju vrijednosti, znakovima $\leq$, $\geq$, $<$, $>$ uspostavlja se \textbf{nejednakost} između dviju vrijednosti. Kao što razlikujemo pojam \emph{jednadžbe} od pojma \emph{jednakosti}, razlikujemo i \emph{nejednadžbu} od \emph{nejednakosti}.
\textit{Primjer 1}
Odredite sve $x\in \mathbb{R}$ za koje je $x^2+2x\leq 0$.
\textit{Rješenje}
Dodavanjem jedinice s obje strane dobivamo da je početna nejednakost ekvivalentna s $(x+1)^2\leq 1$. Ovo je ekvivalentno s $|x+1|\leq 1$. Rješenja nejednadžbe su svi $x\in [-2,0]$.
Kao rješenje upišite najmanji broj koji je rješenje ove nejednadžbe.
 uspostavljamo jednakost nekih dviju vrijednosti, znakovima
uspostavljamo jednakost nekih dviju vrijednosti, znakovima  ,
,  ,
,  ,
,  uspostavlja se nejednakost između dviju vrijednosti. Kao što razlikujemo pojam jednadžbe od pojma jednakosti, razlikujemo i nejednadžbu od nejednakosti.
uspostavlja se nejednakost između dviju vrijednosti. Kao što razlikujemo pojam jednadžbe od pojma jednakosti, razlikujemo i nejednadžbu od nejednakosti.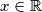 za koje je
za koje je  .
. . Ovo je ekvivalentno s
. Ovo je ekvivalentno s  . Rješenja nejednadžbe su svi
. Rješenja nejednadžbe su svi ![x\in [-2,0]](/media/m/f/e/0/fe04198a93ce1539a466feb3a24877ee.png) .
.