MetaMath '24

U prvom primjeru vidimo kako se rješava nejednadžba. Ono čime ćemo se mi baviti jest dokazivanje nejednakosti. Kada bismo preformulirali prethodni primjer tako da treba dokazati nejednakost, to bi izgledalo ovako: \textit{Primjer 2} Dokažite da vrijedi 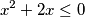\[x^2+2x\leq 0\] za sve $x\in [-2,0]$. \textit{Rješenje} Dodavanjem jedinice s obje strane dobivamo da je nejednakost koju želimo dokazati ekvivalentna s $(x+1)^2\leq 1$. Ovo je ekvivalentno s $|x+1|\leq 1$. Budući da ova nejednakost vrijedi za sve $x\in [-2,0]$, pokazali smo traženu tvrdnju. Kao rješenje napišite najmanji savršeni broj.