Zadatci kojima ćemo se baviti su uglavnom nešto općenitiji - obično trebamo neku tvrdnju pokazati za sve realne ili pozitivne realne brojeve. Pri tome imamo nekoliko korisnih strategija. Prva strategija je svođenje na kvadrate. Ovdje koristimo činjenicu da je  za sve
za sve 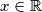 .
.
Primjer 3.
Dokažite da je  za sve
za sve 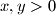 .
.
Rješenje
Množenjem s 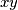 dobivamo da je početna nejednakost ekvivalentna s
dobivamo da je početna nejednakost ekvivalentna s  , odnosno
, odnosno  . To vrijedi jer je kvadrat realnog broja uvijek veći ili jednak nuli.
. To vrijedi jer je kvadrat realnog broja uvijek veći ili jednak nuli.
Oprez!
Kada množimo nejednakost nekim brojem moramo biti pažljivi. Ako je broj kojim množimo pozitivan, smjer nejednakosti ostaje isti, ali ako je negativan smjer nejednakosti se okreće. Na primjer, ako nejednakost  pomnožimo s
pomnožimo s  , ona postaje
, ona postaje  .
.
Kao rjesenje napisite nesto.
Zadatci kojima ćemo se baviti su uglavnom nešto općenitiji - obično trebamo neku tvrdnju pokazati za sve realne ili pozitivne realne brojeve. Pri tome imamo nekoliko korisnih strategija. Prva strategija je svođenje na kvadrate. Ovdje koristimo činjenicu da je $x^2\geq 0$ za sve $x\in \mathbb{R}$.
\textit{Primjer 3.}
Dokažite da je $\frac{x}{y}+\frac{y}{x}\geq 2$ za sve $x,y>0$.
\textit{Rješenje}
Množenjem s $xy$ dobivamo da je početna nejednakost ekvivalentna s $x^2+y^2 \geq 2xy$, odnosno $(x-y)^2\geq 0$. To vrijedi jer je kvadrat realnog broja uvijek veći ili jednak nuli.
\textbf{Oprez!}
Kada množimo nejednakost nekim brojem moramo biti pažljivi. Ako je broj kojim množimo pozitivan, smjer nejednakosti ostaje isti, ali ako je negativan smjer nejednakosti se okreće. Na primjer, ako nejednakost $5\geq -1$ pomnožimo s $-2$, ona postaje $-10\leq 2$.
Kao rjesenje napisite nesto.
 za sve
za sve 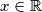 .
. za sve
za sve 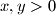 .
.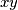 dobivamo da je početna nejednakost ekvivalentna s
dobivamo da je početna nejednakost ekvivalentna s  , odnosno
, odnosno  . To vrijedi jer je kvadrat realnog broja uvijek veći ili jednak nuli.
. To vrijedi jer je kvadrat realnog broja uvijek veći ili jednak nuli. pomnožimo s
pomnožimo s  , ona postaje
, ona postaje  .
.