Sada ćemo predstaviti neke jače nejednakosti koje možemo koristiti pri rješavanju zadataka. Sljedeći teorem poznat je kao nejednakosti među sredinama ili "power mean inequalities".
Teorem 1
Neka su  pozitivni realni brojevi. Vrijedi
pozitivni realni brojevi. Vrijedi  pri čemu jednakost vrijedi ako i samo ako je
pri čemu jednakost vrijedi ako i samo ako je  .
.
Vrijednosti  ,
,  ,
,  i
i  nazivamo redom kvadratna, aritmetička, geometrijska i harmonijska sredina brojeva
nazivamo redom kvadratna, aritmetička, geometrijska i harmonijska sredina brojeva  . Ovaj teorem možete upamtiti ukratko kao "KAGH" nejednakost, a npr. nejednakost između aritmetičke i geometrijske sredine kao AG nejednakost.
. Ovaj teorem možete upamtiti ukratko kao "KAGH" nejednakost, a npr. nejednakost između aritmetičke i geometrijske sredine kao AG nejednakost.
Primjer 4
Neka su 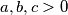 . Dokažite da je
. Dokažite da je 
Rješenje
Iz AG nejednakosti slijedi da je 
 Kada pomnožimo ove dvije nejednakosti dobivamo
Kada pomnožimo ove dvije nejednakosti dobivamo  , pa množenjem s
, pa množenjem s  slijedi tražena nejednakost.
slijedi tražena nejednakost.
Upišite 1. za nastavak.
Sada ćemo predstaviti neke jače nejednakosti koje možemo koristiti pri rješavanju zadataka. Sljedeći teorem poznat je kao nejednakosti među sredinama ili "power mean inequalities".
\textbf{Teorem 1}
Neka su $a_1,\dots , a_n$ pozitivni realni brojevi. Vrijedi
\[\sqrt{\dfrac{a_1^2+\dots +a_n^2}{n}}\geq \dfrac{a_1+\dots +a_n}{n} \geq (a_1\cdots a_n)^{\frac{1}{n}} \geq \dfrac{n}{\frac{1}{a_1}+\dots +\frac{1}{a_n}},\]
pri čemu jednakost vrijedi ako i samo ako je $a_1=a_2=\dots =a_n$.
\\
Vrijednosti $\sqrt{\dfrac{a_1^2+\dots +a_n^2}{n}}$, $\dfrac{a_1+\dots +a_n}{n}$, $(a_1\cdots a_n)^{\frac{1}{n}}$ i $\dfrac{n}{\frac{1}{a_1}+\dots +\frac{1}{a_n}}$ nazivamo redom kvadratna, aritmetička, geometrijska i harmonijska sredina brojeva $a_1,\dots, a_n$. Ovaj teorem možete upamtiti ukratko kao "KAGH" nejednakost, a npr. nejednakost između aritmetičke i geometrijske sredine kao AG nejednakost. \\ \\
\textit{Primjer 4}
Neka su $a,b,c > 0$. Dokažite da je
\[(a^2b+b^2c+c^2a)(ab^2+bc^2+ca^2)\geq 9a^2b^2c^2.\]
\textit{Rješenje}
Iz AG nejednakosti slijedi da je
\[\dfrac{(a^2b+b^2c+c^2a)}{3}\geq (a^2b\cdot b^2c\cdot c^2a)^\frac{1}{3}=(a^3b^3c^3)^\frac{1}{3}=abc \,\,\,\text{ i}\]
\[\dfrac{(ab^2+bc^2+ca^2)}{3}\geq (ab^2bc^2ca^2)^\frac{1}{3}=(a^3b^3c^3)^\frac{1}{3}=abc.\]
Kada pomnožimo ove dvije nejednakosti dobivamo $\dfrac{(a^2b+b^2c+c^2a)(ab^2+bc^2+ca^2)}{9} \geq a^2b^2c^2$, pa množenjem s $9$ slijedi tražena nejednakost.
Upišite 1. za nastavak.
1.
 pozitivni realni brojevi. Vrijedi
pozitivni realni brojevi. Vrijedi  pri čemu jednakost vrijedi ako i samo ako je
pri čemu jednakost vrijedi ako i samo ako je  .
. ,
,  ,
,  i
i  nazivamo redom kvadratna, aritmetička, geometrijska i harmonijska sredina brojeva
nazivamo redom kvadratna, aritmetička, geometrijska i harmonijska sredina brojeva  . Ovaj teorem možete upamtiti ukratko kao "KAGH" nejednakost, a npr. nejednakost između aritmetičke i geometrijske sredine kao AG nejednakost.
. Ovaj teorem možete upamtiti ukratko kao "KAGH" nejednakost, a npr. nejednakost između aritmetičke i geometrijske sredine kao AG nejednakost. 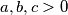 . Dokažite da je
. Dokažite da je 

 Kada pomnožimo ove dvije nejednakosti dobivamo
Kada pomnožimo ove dvije nejednakosti dobivamo  , pa množenjem s
, pa množenjem s  slijedi tražena nejednakost.
slijedi tražena nejednakost.