Vrijeme: 01:53
Nejednakosti - Primjer 5
Teorem 2 (Cauchy-Schwarz)
Neka su  i
i 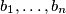 realni brojevi. Vrijedi da je
realni brojevi. Vrijedi da je 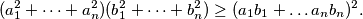
Primjer 5
Dokažite tzv. Engel formu (poznatu i kao Titu lema/T2 lema) CS nejednakosti. Neka su 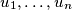 realni i
realni i 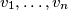 pozitivni realni brojevi. Vrijedi da je
pozitivni realni brojevi. Vrijedi da je 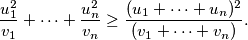
Rješenje
Uzmimo u CS nejednakosti da je 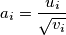 i
i 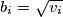 za
za 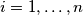 . Dobivamo da je
. Dobivamo da je 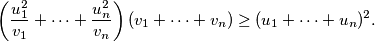 Dijeljenjem s
Dijeljenjem s 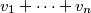 (ovo je pozitivno jer su
(ovo je pozitivno jer su 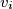 pozitivni) dobivamo traženu nejednakost.
pozitivni) dobivamo traženu nejednakost.
Za nastavak napišite 2.
