Sada imamo "oružja" za dokazivanje nejednakosti. Postoje mnoge druge nejednakosti, npr. Hölderova, Jensenova, težinske nejednakosti među sredinama, rearrangement i još brojne druge. U ovom pdf-u zadržat ćemo se na osnovama. Iako je korisno znati puno različitih nejednakosti, vidjet ćete da su već i osnovne nejednakosti vrlo moćan alat i da je potrebno puno znanja i vještine da bi se pravilno upotrijebile.
U praksi najčešće je dovoljno znati AG nejednakost. Međutim, primjena te nejednakosti zahtijeva dobro razumijevanje njene pravilne primjene. Treba znati da su sve dosad navedene nejednakosti homogene, što znači da su eksponenti pribrojnika s lijeve i desne strane isti (npr. eksponenti od 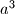 ,
, 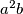 ,
,  i
i 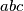 su svi
su svi  ). Ako je nejednakost koju pokazujemo nehomogena, često je dan uvjet kojim se ta nejednakost može svesti na homogeni oblik. Pogledajmo kako to izgleda u praksi.
). Ako je nejednakost koju pokazujemo nehomogena, često je dan uvjet kojim se ta nejednakost može svesti na homogeni oblik. Pogledajmo kako to izgleda u praksi.
Primjer 6
Dokažite da za sve 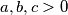 za koje je
za koje je 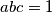 vrijedi
vrijedi  .
.
Rješenje
Da bismo homogenizirali ovu nejednakost pomnožimo desnu stranu s ![\sqrt[3]{abc}](/media/m/0/d/9/0d935cc078e009b3095a7c8f54f0c784.png) . Početna nejednakost je ekvivalentna s
. Početna nejednakost je ekvivalentna s  .
.
Iz AG nejednakosti slijedi da je  Zbrajanjem ovih triju nejednakosti dobivamo traženu nejednakost.
Zbrajanjem ovih triju nejednakosti dobivamo traženu nejednakost.
A sad - AJMOOO! (kao rješenje možete upisati IDEMOOO)
Sada imamo "oružja" za dokazivanje nejednakosti. Postoje mnoge druge nejednakosti, npr. \href{https://artofproblemsolving.com/wiki/index.php/Hölder%27s_Inequality}{Hölderova}, \href{https://artofproblemsolving.com/wiki/index.php/Jensen%27s_Inequality}{Jensenova}, \href{https://planetmath.org/weightedpowermean}{težinske nejednakosti među sredinama}, \href{https://en.wikipedia.org/wiki/Rearrangement_inequality}{rearrangement} i još brojne druge. U ovom pdf-u zadržat ćemo se na osnovama. Iako je korisno znati puno različitih nejednakosti, vidjet ćete da su već i osnovne nejednakosti vrlo moćan alat i da je potrebno puno znanja i vještine da bi se pravilno upotrijebile.
U praksi najčešće je dovoljno znati AG nejednakost. Međutim, primjena te nejednakosti zahtijeva dobro razumijevanje njene pravilne primjene. Treba znati da su sve dosad navedene nejednakosti \emph{homogene}, što znači da su eksponenti pribrojnika s lijeve i desne strane isti (npr. eksponenti od $a^3$, $a^2b$, $ac^2$ i $abc$ su svi $3$). Ako je nejednakost koju pokazujemo \emph{nehomogena}, često je dan uvjet kojim se ta nejednakost može svesti na homogeni oblik. Pogledajmo kako to izgleda u praksi.
\emph{Primjer 6}
Dokažite da za sve $a,b,c > 0$ za koje je $abc=1$ vrijedi $a^2+b^2+c^2\geq a+b+c$.
\emph{Rješenje}
Da bismo homogenizirali ovu nejednakost pomnožimo desnu stranu s $\sqrt[3]{abc}$. Početna nejednakost je ekvivalentna s $a^2+b^2+c^2\geq a^\frac{1}{3}b^\frac{1}{3}c^\frac{1}{3}(a+b+c)=a^\frac{4}{3}b^\frac{1}{3}c^\frac{1}{3}+a^\frac{1}{3}b^\frac{4}{3}c^\frac{1}{3}+a^\frac{1}{3}b^\frac{1}{3}c^\frac{4}{3}$.
Iz AG nejednakosti slijedi da je \begin{align*}
\dfrac{4a^2+b^2+c^2}{6}=\dfrac{a^2+a^2+a^2+a^2+b^2+c^2}{6} & \geq (a^8b^2c^2)^\frac{1}{6}= a^\frac{4}{3}b^\frac{1}{3}c^\frac{1}{3},\\
\dfrac{a^2+4b^2+c^2}{6}=\dfrac{a^2+b^2+b^2+b^2+b^2+c^2}{6} & \geq (a^2b^8c^2)^\frac{1}{6}= a^\frac{1}{3}b^\frac{4}{3}c^\frac{1}{3},\\
\dfrac{a^2+b^2+4c^2}{6}=\dfrac{a^2+b^2+c^2+c^2+c^2+c^2}{6} & \geq (a^2b^2c^8)^\frac{1}{6}= a^\frac{1}{3}b^\frac{1}{3}c^\frac{4}{3}.
\end{align*}
Zbrajanjem ovih triju nejednakosti dobivamo traženu nejednakost.
A sad - AJMOOO! (kao rješenje možete upisati IDEMOOO)
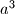 ,
, 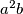 ,
,  i
i 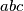 su svi
su svi  ). Ako je nejednakost koju pokazujemo nehomogena, često je dan uvjet kojim se ta nejednakost može svesti na homogeni oblik. Pogledajmo kako to izgleda u praksi.
). Ako je nejednakost koju pokazujemo nehomogena, često je dan uvjet kojim se ta nejednakost može svesti na homogeni oblik. Pogledajmo kako to izgleda u praksi.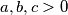 za koje je
za koje je 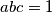 vrijedi
vrijedi  .
.![\sqrt[3]{abc}](/media/m/0/d/9/0d935cc078e009b3095a7c8f54f0c784.png) . Početna nejednakost je ekvivalentna s
. Početna nejednakost je ekvivalentna s  .
. Zbrajanjem ovih triju nejednakosti dobivamo traženu nejednakost.
Zbrajanjem ovih triju nejednakosti dobivamo traženu nejednakost.