MetaMath '24

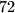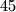\textbf{Zadatak:}\\ Odredi mjeru brojeva $72$ i $45$.\\ \textbf{Rješenje:}\\ $gcd(72, 45) = gcd(27, 45) = gcd(27, 18) = gcd(9, 18) = gcd(9, 9) = 9$\\ Ovo je jako jednostavan primjer jer pričamo o konstantama, ali možete vidjeti da je jako slično kad uvedemo i neke varijable:\\ \textbf{Zadatak:}\\ Dokaži da se razlomak 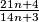$\frac{21n + 4}{14n + 3}$ ne može skratiti, ako je $n \in \mathbb{N}$.\\ \textbf{Rješenje:}\\ Kada bi se taj razlomak mogao skratiti, onda bi postojao neki prirodni broj veći od $1$ koji dijeli i brojnik i nazivnik. Mi želimo pokazati da takav broj ne postoji, odnosno da su brojnik i nazivnik relativno prosti. Kako su oba zapisana u istoj varijabli($n$) možemo lagano koristiti Euklidov algoritam na njima i vidjeti dokle će nas to dovesti.\\ $gcd(21n + 4, 14n + 3) = gcd(7n + 1, 14n + 3) = gcd(7n + 1, 7n + 2) = gcd(7n + 1, 1) = 1$.\\ Zaključujemo da su brojnik i nazivnik relativno prosti, odnosno da ne postoji neki broj koji ih oba dijeli pa se razlomak ne može skratiti.\\ A sada slijedi nešto što bismo čak i mogli nazvati teoremom, a lagano se pokaže da vrijedi primjenom Euklida:\\ \textbf{Teorem:}\\ Uzastopni prirodni brojevi su relativno prosti.\\ \textbf{Dokaz}:\\ Uzmimo proizvoljan par uzastopnih prirodnih brojeva i označimo ih s $n$ i $n + 1$. 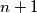Računamo njihovu mjeru: $gcd(n, n + 1) = gcd(n, 1) = 1$.\\ \textbf{Zadatak za rješavanje:}\\ Odredite $gcd(150, 60)$