Napokon idemo na jedan jako zanimljiv podskup prirodnih brojeva, prosti brojevi.
Definicija: Za prirodan broj kažemo da je prost ako ima točno  djelitelja. Za sve ostale prirodne brojeve kažemo da su složeni, osim
djelitelja. Za sve ostale prirodne brojeve kažemo da su složeni, osim  , koji nije ni prost ni složen.
, koji nije ni prost ni složen.
Prosti brojevi su jako zanimljivi i jedna od temeljnih tema u teoriji brojeva. Njih ćete jako često susretati tako da predstavljam neka njihova svojstva:
Teorem:
Svaki prirodni broj ima jedinstveni rastav na proste faktore.
Ovo ste vjerojatno vidjeli u školi i to je manje više samo onaj rastav na proste faktore, popularno zvan "čizma". Ponovno ćete kao i kod Euklidovog algoritma više koristiti to samo kao alat traženja rastava na proste faktore.
I time dolazimo do lema koja se možda ne čini tako, ali daje jako veliku snagu prostim brojevima:
Lema:
Neka je  prost i
prost i  i
i  prirodni. Ako
prirodni. Ako 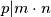 , onda
, onda 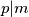 ili
ili 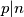 .
.
Mi ćemo ju prihvatiti kao aksiom, ali opet intuitivno vidite kako to mora vrijediti zato što  nema nikakve djelitelje osim samog sebe pa te djelitelje ne možemo "rasporediti" na
nema nikakve djelitelje osim samog sebe pa te djelitelje ne možemo "rasporediti" na  i
i  nego cijeli
nego cijeli  dijeli jednog od njih.
dijeli jednog od njih.
Zadatak:
Odredite sve proste  takve da vrijedi:
takve da vrijedi: 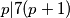 .
.
Rješenje:
Znamo da mora vrijediti 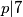 ili
ili 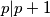 . Pretpostavimo prvo da
. Pretpostavimo prvo da 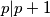 , sada imamo
, sada imamo 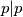 (svaki broj trivijalno dijeli sam sebe) i
(svaki broj trivijalno dijeli sam sebe) i 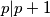 , odnosno
, odnosno 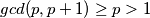 . To ne može biti jer su ozastopni brojevi relativno prosti pa dolazimo u kontradikciju i zaključujemo da
. To ne može biti jer su ozastopni brojevi relativno prosti pa dolazimo u kontradikciju i zaključujemo da 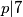 . Kako je
. Kako je  i sam prost mora vrijediti
i sam prost mora vrijediti 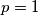 ili
ili 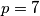 , no
, no  nije prost i dolazimo do zaključka da je
nije prost i dolazimo do zaključka da je 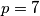 jedino rješenje.
jedino rješenje.
Kao odgovor na ovo pitanje napišite koji je najveći prosti broj koji dijeli  .
.
Napokon idemo na jedan jako zanimljiv podskup prirodnih brojeva, prosti brojevi.
\textbf{Definicija:}
Za prirodan broj kažemo da je prost ako ima točno $2$ djelitelja. Za sve ostale prirodne brojeve kažemo da su složeni, osim $1$, koji nije ni prost ni složen.\\
Prosti brojevi su jako zanimljivi i jedna od temeljnih tema u teoriji brojeva. Njih ćete jako često susretati tako da predstavljam neka njihova svojstva:\\
\textbf{Teorem:}\\
Svaki prirodni broj ima jedinstveni rastav na proste faktore.\\
Ovo ste vjerojatno vidjeli u školi i to je manje više samo onaj rastav na proste faktore, popularno zvan "čizma". Ponovno ćete kao i kod Euklidovog algoritma više koristiti to samo kao alat traženja rastava na proste faktore.\\
I time dolazimo do lema koja se možda ne čini tako, ali daje jako veliku snagu prostim brojevima:\\
\textbf{Lema:}\\
Neka je $p$ prost i $m$ i $n$ prirodni. Ako $p|m\cdot n$, onda $p|m$ ili $p|n$.\\
Mi ćemo ju prihvatiti kao aksiom, ali opet intuitivno vidite kako to mora vrijediti zato što $p$ nema nikakve djelitelje osim samog sebe pa te djelitelje ne možemo "rasporediti" na $m$ i $n$ nego cijeli $p$ dijeli jednog od njih.\\
\textbf{Zadatak:}\\
Odredite sve proste $p$ takve da vrijedi: $p | 7(p + 1)$.\\
\textbf{Rješenje:}\\
Znamo da mora vrijediti $p | 7$ ili $p | p + 1$. Pretpostavimo prvo da $p | p + 1$, sada imamo $p | p $ (svaki broj trivijalno dijeli sam sebe) i $p | p + 1$, odnosno $gcd(p, p + 1) \geq p > 1$. To ne može biti jer su ozastopni brojevi relativno prosti pa dolazimo u kontradikciju i zaključujemo da $p | 7$. Kako je $7$ i sam prost mora vrijediti $p = 1$ ili $p = 7$, no $1$ nije prost i dolazimo do zaključka da je $p = 7$ jedino rješenje.
Kao odgovor na ovo pitanje napišite koji je najveći prosti broj koji dijeli $11$.
 djelitelja. Za sve ostale prirodne brojeve kažemo da su složeni, osim
djelitelja. Za sve ostale prirodne brojeve kažemo da su složeni, osim  , koji nije ni prost ni složen.
, koji nije ni prost ni složen. prost i
prost i  i
i  prirodni. Ako
prirodni. Ako 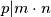 , onda
, onda 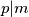 ili
ili 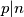 .
. nema nikakve djelitelje osim samog sebe pa te djelitelje ne možemo "rasporediti" na
nema nikakve djelitelje osim samog sebe pa te djelitelje ne možemo "rasporediti" na  i
i  nego cijeli
nego cijeli  dijeli jednog od njih.
dijeli jednog od njih. takve da vrijedi:
takve da vrijedi: 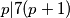 .
.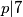 ili
ili 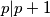 . Pretpostavimo prvo da
. Pretpostavimo prvo da 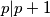 , sada imamo
, sada imamo 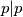 (svaki broj trivijalno dijeli sam sebe) i
(svaki broj trivijalno dijeli sam sebe) i 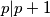 , odnosno
, odnosno 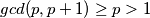 . To ne može biti jer su ozastopni brojevi relativno prosti pa dolazimo u kontradikciju i zaključujemo da
. To ne može biti jer su ozastopni brojevi relativno prosti pa dolazimo u kontradikciju i zaključujemo da 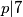 . Kako je
. Kako je  i sam prost mora vrijediti
i sam prost mora vrijediti 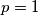 ili
ili 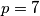 , no
, no  nije prost i dolazimo do zaključka da je
nije prost i dolazimo do zaključka da je 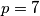 jedino rješenje.
jedino rješenje. .
. 