Na kraju dolazimo do kanonskog zapisa i načina za računanje broja djelitelja od  . Kanonski zapis je samo uljepšani način za reći/zapisati rastav na proste faktore nekog prirodnog broja. Za nepoznati broj
. Kanonski zapis je samo uljepšani način za reći/zapisati rastav na proste faktore nekog prirodnog broja. Za nepoznati broj  ga zapisujemo ovako:
ga zapisujemo ovako:  , gdje su
, gdje su 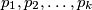 različiti prosti brojevi koji dijele
različiti prosti brojevi koji dijele  , a
, a  odgovarajuće potencije tih prostih brojeva. Vratimo se na primjer od
odgovarajuće potencije tih prostih brojeva. Vratimo se na primjer od 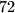 , njega možemo zapisati kao
, njega možemo zapisati kao  . Najpametnije stvari koje nam ovaj zapis daje jest sama djeljivost broja
. Najpametnije stvari koje nam ovaj zapis daje jest sama djeljivost broja  s nekim od
s nekim od  , ali također i broj djelitelja od
, ali također i broj djelitelja od  . E sada, da iz tog zapisa dođemo do broja djelitelja trebamo malo primjene kombinatorike. Znamo da će se djelitelj od
. E sada, da iz tog zapisa dođemo do broja djelitelja trebamo malo primjene kombinatorike. Znamo da će se djelitelj od  morati sastojati od nekih kombinacija potencija prostih brojeva koje dijele
morati sastojati od nekih kombinacija potencija prostih brojeva koje dijele  i također znamo da potencija prostog broja koja dijeli djelitelja od
i također znamo da potencija prostog broja koja dijeli djelitelja od  ne smije biti veća od potencije istog tog prostog broja koja dijeli
ne smije biti veća od potencije istog tog prostog broja koja dijeli  . Promatrajmo to na primjeru
. Promatrajmo to na primjeru 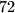 . Nekog djelitelja od
. Nekog djelitelja od 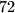 prost broj
prost broj  može dijeliti
može dijeliti  ,
,  ,
,  i
i  puta, što su ukupno
puta, što su ukupno  kombinacije. Nadalje, prost broj
kombinacije. Nadalje, prost broj  ga može dijeliti
ga može dijeliti  ,
,  ili
ili  puta i to su
puta i to su  kombinacije. To nam daje da je ukupan broj djelitelja od
kombinacije. To nam daje da je ukupan broj djelitelja od 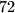 jednak
jednak  . Za proizvoljan
. Za proizvoljan  broj djelitelja bit će dan formulom:
broj djelitelja bit će dan formulom:  .
.
Vjerujem da će vam biti jasnije nakon primjera:
Zadatak: Koliko djelitelja ima broj 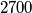 ?
?
Rješenje:
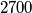 možemo zapisati kao
možemo zapisati kao  pa računamo da je broj njegovih djelitelja jednak
pa računamo da je broj njegovih djelitelja jednak  .
.
Zadatak:
Odredi sve prirodne  koji su djeljivi s
koji su djeljivi s  i
i  i imaju točno
i imaju točno 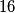 djelitelja.
djelitelja.
Rješenje:
Uzmimo  . Znamo da je broj djelitelja jednak
. Znamo da je broj djelitelja jednak  pa pišemo
pa pišemo 
 i
i  su cijeli brojevi, pa su i
su cijeli brojevi, pa su i  i
i  cijeli brojevi, pa sada želimo samo gledati koje kombinacije umnožaka daju
cijeli brojevi, pa sada želimo samo gledati koje kombinacije umnožaka daju 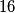 . Rastav od
. Rastav od 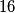 na proste faktore je
na proste faktore je  što nam daje da su moguće kombinacije za
što nam daje da su moguće kombinacije za  i
i  :
:  ,
,  ,
,  ,
,  ,
,  . Oduzimanjem jedinica dobivamo kombinacije za
. Oduzimanjem jedinica dobivamo kombinacije za  i
i  :
:  ,
,  ,
,  ,
,  ,
,  . Odnosno brojevi koji zadovoljavaju uvjete zadatka su:
. Odnosno brojevi koji zadovoljavaju uvjete zadatka su:  ,
,  ,
,  ,
,  ,
,  .
.
Nakon ovih primjera, kao rješenje napišite koliko djelitelja ima  ?
?
Na kraju dolazimo do kanonskog zapisa i načina za računanje broja djelitelja od $n$. Kanonski zapis je samo uljepšani način za reći/zapisati rastav na proste faktore nekog prirodnog broja. Za nepoznati broj $n$ ga zapisujemo ovako: $n = p_1^{\alpha _1}\cdot p_2^{\alpha _2} \cdot \dots \cdot p_k^{\alpha _k}$, gdje su $p_1, p_2, \dots, p_k$ različiti prosti brojevi koji dijele $n$, a $\alpha_1, \alpha_2, \dots, \alpha_k$ odgovarajuće potencije tih prostih brojeva. Vratimo se na primjer od $72$, njega možemo zapisati kao $72 = 2^3\cdot3^2$. Najpametnije stvari koje nam ovaj zapis daje jest sama djeljivost broja $n$ s nekim od $p_i^{\alpha_i}$, ali također i broj djelitelja od $n$. E sada, da iz tog zapisa dođemo do broja djelitelja trebamo malo primjene kombinatorike. Znamo da će se djelitelj od $n$ morati sastojati od nekih kombinacija potencija prostih brojeva koje dijele $n$ i također znamo da potencija prostog broja koja dijeli djelitelja od $n$ ne smije biti veća od potencije istog tog prostog broja koja dijeli $n$. Promatrajmo to na primjeru $72$. Nekog djelitelja od $72$ prost broj $2$ može dijeliti $0$, $1$, $2$ i $3$ puta, što su ukupno $4$ kombinacije. Nadalje, prost broj $3$ ga može dijeliti $0$, $1$ ili $2$ puta i to su $3$ kombinacije. To nam daje da je ukupan broj djelitelja od $72$ jednak $4 \cdot 3 = 12$. Za proizvoljan $n = p_1^{\alpha _1}\cdot p_2^{\alpha _2} \cdot \dots \cdot p_k^{\alpha _k}$ broj djelitelja bit će dan formulom: $(\alpha_1 + 1)(\alpha_2 + 1)\dots(\alpha_k + 1)$.\\
Vjerujem da će vam biti jasnije nakon primjera:\\
\textbf{Zadatak:}
Koliko djelitelja ima broj $2700$?\\
\textbf{Rješenje:}\\
$2700$ možemo zapisati kao $2^2 \cdot 3^3 \cdot 5^2$ pa računamo da je broj njegovih djelitelja jednak $3\cdot 4\cdot 3 = 36$.\\
\textbf{Zadatak:}\\
Odredi sve prirodne $n$ koji su djeljivi s $2$ i $3$ i imaju točno $16$ djelitelja.\\
\textbf{Rješenje:}\\
Uzmimo $n = 2^{\alpha_1} \cdot 3^{\alpha_2}$. Znamo da je broj djelitelja jednak $(\alpha_1 + 1)(\alpha_2 + 1)$ pa pišemo $$(\alpha_1 + 1)(\alpha_2 + 1) = 16$$
$\alpha_1$ i $\alpha_2$ su cijeli brojevi, pa su i $\alpha_1 + 1$ i $\alpha_2 + 1$ cijeli brojevi, pa sada želimo samo gledati koje kombinacije umnožaka daju $16$. Rastav od $16$ na proste faktore je $2^4$ što nam daje da su moguće kombinacije za $\alpha_1 + 1$ i $\alpha_2 + 1$: $(1, 16)$, $(2, 8)$, $(4, 4)$, $(8, 2)$, $(16, 1)$. Oduzimanjem jedinica dobivamo kombinacije za $\alpha_1$ i $\alpha_2$: $(0, 15)$, $(1, 7)$, $(3, 3)$, $(7, 1)$, $(15, 0)$. Odnosno brojevi koji zadovoljavaju uvjete zadatka su: $2^0\cdot3^15 = 14348907$, $2^1\cdot3^7 = 4374$, $2^3\cdot3^3 = 216$, $2^7\cdot3^1 = 384$, $2^15\cdot3^0 = 32768$.\\
Nakon ovih primjera, kao rješenje napišite koliko djelitelja ima $750$?
 . Kanonski zapis je samo uljepšani način za reći/zapisati rastav na proste faktore nekog prirodnog broja. Za nepoznati broj
. Kanonski zapis je samo uljepšani način za reći/zapisati rastav na proste faktore nekog prirodnog broja. Za nepoznati broj  ga zapisujemo ovako:
ga zapisujemo ovako:  , gdje su
, gdje su 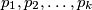 različiti prosti brojevi koji dijele
različiti prosti brojevi koji dijele  , a
, a  odgovarajuće potencije tih prostih brojeva. Vratimo se na primjer od
odgovarajuće potencije tih prostih brojeva. Vratimo se na primjer od 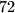 , njega možemo zapisati kao
, njega možemo zapisati kao  . Najpametnije stvari koje nam ovaj zapis daje jest sama djeljivost broja
. Najpametnije stvari koje nam ovaj zapis daje jest sama djeljivost broja  s nekim od
s nekim od  , ali također i broj djelitelja od
, ali također i broj djelitelja od  . E sada, da iz tog zapisa dođemo do broja djelitelja trebamo malo primjene kombinatorike. Znamo da će se djelitelj od
. E sada, da iz tog zapisa dođemo do broja djelitelja trebamo malo primjene kombinatorike. Znamo da će se djelitelj od  morati sastojati od nekih kombinacija potencija prostih brojeva koje dijele
morati sastojati od nekih kombinacija potencija prostih brojeva koje dijele  i također znamo da potencija prostog broja koja dijeli djelitelja od
i također znamo da potencija prostog broja koja dijeli djelitelja od  ne smije biti veća od potencije istog tog prostog broja koja dijeli
ne smije biti veća od potencije istog tog prostog broja koja dijeli  . Promatrajmo to na primjeru
. Promatrajmo to na primjeru 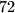 . Nekog djelitelja od
. Nekog djelitelja od 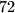 prost broj
prost broj  može dijeliti
može dijeliti  ,
,  ,
,  i
i  puta, što su ukupno
puta, što su ukupno  kombinacije. Nadalje, prost broj
kombinacije. Nadalje, prost broj  ga može dijeliti
ga može dijeliti  ,
,  ili
ili  puta i to su
puta i to su  kombinacije. To nam daje da je ukupan broj djelitelja od
kombinacije. To nam daje da je ukupan broj djelitelja od 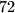 jednak
jednak  . Za proizvoljan
. Za proizvoljan  broj djelitelja bit će dan formulom:
broj djelitelja bit će dan formulom:  .
.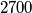 ?
?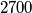 možemo zapisati kao
možemo zapisati kao  pa računamo da je broj njegovih djelitelja jednak
pa računamo da je broj njegovih djelitelja jednak  .
. koji su djeljivi s
koji su djeljivi s  i
i  i imaju točno
i imaju točno 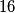 djelitelja.
djelitelja. . Znamo da je broj djelitelja jednak
. Znamo da je broj djelitelja jednak  pa pišemo
pa pišemo 
 i
i  su cijeli brojevi, pa su i
su cijeli brojevi, pa su i  i
i  cijeli brojevi, pa sada želimo samo gledati koje kombinacije umnožaka daju
cijeli brojevi, pa sada želimo samo gledati koje kombinacije umnožaka daju 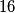 . Rastav od
. Rastav od 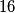 na proste faktore je
na proste faktore je  što nam daje da su moguće kombinacije za
što nam daje da su moguće kombinacije za  i
i  :
:  ,
,  ,
,  ,
,  ,
,  . Oduzimanjem jedinica dobivamo kombinacije za
. Oduzimanjem jedinica dobivamo kombinacije za  i
i  :
:  ,
,  ,
,  ,
,  ,
,  . Odnosno brojevi koji zadovoljavaju uvjete zadatka su:
. Odnosno brojevi koji zadovoljavaju uvjete zadatka su:  ,
,  ,
,  ,
,  ,
,  .
. ?
? 