MetaMath '24

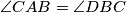Dokazat ćemo poučak o kutu između tetive i tangente. Neka je $BC$ dana tetiva i točka $A$ na kružnici. Točka $D$ se nalazi na tangenti sa suprotne strane dužine $BC$ u odnosu na točku $A$. Trebamo dokazati $\angle CAB=\angle DBC$. Odmah možemo primjetiti da je kut 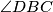$\angle DBC$ dosta "nedohvatljiv" jer nije u nikakvom trokutu. niti je obodni kut, nemamo puno načina za povezati ga s drugim elementima skice i drukčije izraziti. 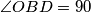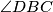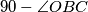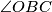Jedino nam preostaje iskoristiti kut tangente, odnosno to da $\angle OBD=90$ i to nam odgovara jer možemo $\angle DBC$ izraziti kao $90-\angle OBC$, a $\angle OBC$ je "pristupačniji", tj. bolje je povezan s ostatkom skice i upravo to ćemo iskoristiti. U geometriji često zadatak treba sagledati s poečetka i s kraja, u svakom koraku trebamo pratiti što smo dobili i što nam je potrebno za završiti zadatak. Tu kada gledamo s kraja vidimo da nam nije lagano direktno povezati kut 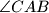$\angle CAB$ s kutom 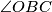$\angle OBC$, ali možemo ih povezati preko kuta 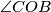$\angle COB$. Iz teorema o središnjem i obodnom kutu 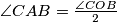$\angle CAB=\frac{\angle COB}{2}$. Iz toga što je 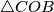$\triangle COB$ jednakokračan dobivamo 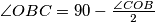$\angle OBC=90-\frac{\angle COB}{2}$. Sada imamo 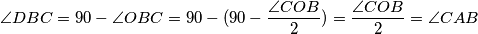$$\angle DBC=90-\angle OBC=90-(90-\frac{\angle COB}{2} )=\frac{\angle COB}{2}=\angle CAB$$. A upravo to smo i trebali dokazati. Za nastavak upišite 1.