Neka je $I$ središte upisane kružnice trokuta $\triangle ABC$. Dokaži da vrijedi: $\angle BIC = 90+ \dfrac{\angle BAC}{2}$.
Promatrat ćemo $\triangle BIC$ jer sadrži kut koji želimo izračunati i "povezan" je s $\triangle ABC$ preko točaka $B,C$. Dobivamo: $\angle BIC=180- \angle ICB - \angle CBI$. Središte upisane kružnice je sjecište simetrala kuteva trokuta pa vrijedi: $\angle ICB = \frac{\angle ACB}{2}$ i $\angle CBI = \frac{\angle CBA}{2}$. Iz $\triangle ABC$ znamo $ \angle ACB + \angle CBA = 180 - \angle BAC \Longrightarrow \frac{\angle ACB + \angle CBA }{2} = 90 - \frac{ \angle BAC }{2} $ Sada uvrštavanjem dobivenog dobivamo: $\angle BIC=180-\frac{\angle ACB}{2}-\frac{\angle CBA}{2}=180-\frac{180-\angle BAC}{2}=90+ \frac{ \angle BAC }{2}$.
Za nastavak upišite 1.
 središte upisane kružnice trokuta
središte upisane kružnice trokuta  . Dokaži da vrijedi:
. Dokaži da vrijedi:  .
. jer sadrži kut koji želimo izračunati i "povezan" je s
jer sadrži kut koji želimo izračunati i "povezan" je s  preko točaka
preko točaka 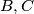 . Dobivamo:
. Dobivamo:  . Središte upisane kružnice je sjecište simetrala kuteva trokuta pa vrijedi:
. Središte upisane kružnice je sjecište simetrala kuteva trokuta pa vrijedi:  i
i  . Iz
. Iz  znamo
znamo  Sada uvrštavanjem dobivenog dobivamo:
Sada uvrštavanjem dobivenog dobivamo:  .
.