MetaMath '24

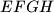Dan je četverokut $ABCD$, simetrale unutarnjih kutova vrhova $(A,B), (B,C), (C,D), (D,A)$ sijeku se redom u točkama $E, F, G, H$. Dokaži da je četverokut $EFGH$ tetivan. U ovom slučaju najlakše ćemo dokazati tetivnost preko zbroja nasuprotinih kutova. Na to nam ukazuje sama definicija tih kutova jer su zadani pomoću simetrala početnog kuta, tj. suplementarni su kutovima koji su u trokutu omeđenom simetralama kutova, a u prvom primjeru smo vidjeli da se u takvom trokutu kutovi lako izračunaju. Drugi hint nam je to što se dodavanje dijagonala za drugačiji pristup čini dosta nespretno jer dodajemo nove elemente koje ne možemo uklopiti u sadašnju skicu s računske strane. Kako je skica simetrična, svejedno je koje ćemo kutove odabrati. Mi ćemo doakazati da $\angle HEF+ \angle FGH=180 \longleftrightarrow 180-\angle AEB+ 180-\angle DGC=180 \longleftrightarrow \angle AEB+\angle DGC=180 $. Iz $\triangle AEB$ znamo $\angle AEB=180-\frac{\angle DAB+\angle ABC}{2}$, iz $\triangle DGC$ znamo $\angle DGC=180-\frac{\angle BCD+\angle CDA}{2} \longrightarrow \angle AEB+\angle DGC=360-\frac{\angle DAB+\angle ABC+\angle BCD+\angle CDA}{2}=180$ jer je zbroj kutova u $ABCD$ jednak 360 i time smo dovršili dokaz. Za nastavak upišite 1