Vrijeme: 01:53
Angle chase- Primjer 3
Neka je  promjer kružnice
promjer kružnice  i neka su
i neka su  ,
,  na luku
na luku  . Neka je
. Neka je  presjek pravaca
presjek pravaca 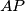 i
i 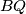 , a
, a  presjek pravaca
presjek pravaca 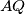 i
i 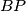 . Dokažite da je
. Dokažite da je  .
.
Dokaz:
Bez smanjenja općenitosti, pravci  i
i  sijeku se unutar kružnice, a
sijeku se unutar kružnice, a  i
i  izvan.
izvan.
Po Talesovom poučku  . Sada možemo primjetiti da su
. Sada možemo primjetiti da su  i
i  su visine
su visine  .
.
Tada je N ortocentar (sjecište visina) u  . Znamo da onda i visina iz vrha
. Znamo da onda i visina iz vrha  mora prolaziti kroz točku
mora prolaziti kroz točku pa je ta visina upravo pravac
pa je ta visina upravo pravac  i zbog toga je okomit na
i zbog toga je okomit na 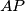 .
.
Za nastavak upišite 1.
