Zadatak: U dvorani se nalazi  stolaca u istom redu, označenih prirodnim brojevima od
stolaca u istom redu, označenih prirodnim brojevima od  do
do  . Mentori pripremaju učionicu za sastanak tako što stavljaju oznake na stolce na koje će
. Mentori pripremaju učionicu za sastanak tako što stavljaju oznake na stolce na koje će  učenika smjeti sjesti. Koliko ima odabira stolaca ako znamo da učenici ne smiju sjesti jedan do drugoga?
učenika smjeti sjesti. Koliko ima odabira stolaca ako znamo da učenici ne smiju sjesti jedan do drugoga?

Rješenje:
U ovom zadatku zapravo nam je najveći problem to što učenici ne smiju sjediti jedan do drugoga. Kad tog uvjeta ne bismo imali, postupili bismo kao u videu profesorice Zelčić:

Prvo bismo odabrali  različitih stolaca razmišljajući ovako:
različitih stolaca razmišljajući ovako: 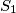 možemo odabrati na
možemo odabrati na  načina,
načina, 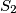 možemo odabrati na
možemo odabrati na  načina,
načina, 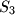 možemo odabrati na
možemo odabrati na  načina, i tako sve do
načina, i tako sve do 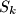 , kojeg možemo odabrati na
, kojeg možemo odabrati na 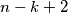 načina. Kako stolci ipak nisu različiti, svaki odabir stolaca smo brojali više puta. Zato rezultat treba podijeliti s
načina. Kako stolci ipak nisu različiti, svaki odabir stolaca smo brojali više puta. Zato rezultat treba podijeliti s 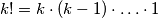 , jer se svaki odabir stolaca pojavljuje onoliko puta koliko je različitih poredaka
, jer se svaki odabir stolaca pojavljuje onoliko puta koliko je različitih poredaka  stolaca. Njih je
stolaca. Njih je 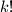 jer prvog možemo odabrati na
jer prvog možemo odabrati na  načina, drugog na
načina, drugog na  , i tako dalje.
, i tako dalje.
Nažalost, u ovom zadatku imam ograničenje: učenici ne mogu sjediti jedan kraj drugog. Kako mu doskočiti? Jedna od prvih ideja koje bi nam mogle pasti napamet je idemo uz stolac blokirati i njegove susjede, dakle postupimo kao u drugom primjeru kada smo braću Grim tretirali kao jedno biće koje sjedi na  stolca. Nažalost, to nije dobro, jer bismo tada u slučaju učenik - prazno - učenik prazninu u sredini blokirali dvaput.
stolca. Nažalost, to nije dobro, jer bismo tada u slučaju učenik - prazno - učenik prazninu u sredini blokirali dvaput.

Kako ćemo onda doskočiti problemu? Označimo prvo  stolaca: prvih
stolaca: prvih  stolaca bit će nam stolci na koje učenici nikako ne smiju sjesti (stolci između učenika), a zadnji je stolac gdje sjedi zadnji učenik. Između svih oznaka mora postojati razmak osim zadnje.
stolaca bit će nam stolci na koje učenici nikako ne smiju sjesti (stolci između učenika), a zadnji je stolac gdje sjedi zadnji učenik. Između svih oznaka mora postojati razmak osim zadnje.

Prvi učenik sjedne neposredno prije prve oznake, drugi neposredno prije druge, ..., dok zadnji sjedne gdje je određeno.
Sada kao u prethodnom primjeru vidimo da je takvih odabira isto koliko zbrojeva 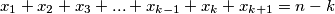 gdje
gdje 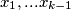 moraju biti pozitivni, a ostala 2 nenegativna (
moraju biti pozitivni, a ostala 2 nenegativna ( predstavlja broj sjedala između
predstavlja broj sjedala između  oznake, s tim da je
oznake, s tim da je 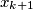 broj sjedala iza zadnje oznake.).
broj sjedala iza zadnje oznake.).
Sada koristimo mali trik kako bismo primijenili formulu izvedenu u prošlom zadatku. Označimo 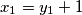 ,
, 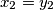 ,
, 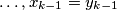 , a zadnja
, a zadnja  ostavljamo iste (
ostavljamo iste (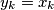 ,
, 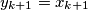 ).
).
Prikazujući gornju jednadžbu preko varijable  jednadžba postaje:
jednadžba postaje: 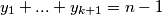 gdje su
gdje su 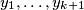 nenegativni brojevi, što se lako dobije po formuli izvedenom u primjeru
nenegativni brojevi, što se lako dobije po formuli izvedenom u primjeru  .
.
Kao rješenje upišite "jiayou" (na kineskom: 加油).
\textbf{Zadatak:} U dvorani se nalazi $n$ stolaca u istom redu, označenih prirodnim brojevima od $1$ do $n$. Mentori
pripremaju učionicu za sastanak tako što stavljaju oznake na stolce na koje će $k$ učenika smjeti sjesti. Koliko
ima odabira stolaca ako znamo da učenici ne smiju sjesti jedan do drugoga?
\\
\includegraphics{pr51.png}
\\
\textbf{Rješenje:}
U ovom zadatku zapravo nam je najveći problem to što učenici ne smiju sjediti jedan do drugoga. Kad tog uvjeta ne bismo imali, postupili bismo kao u videu profesorice Zelčić:
\\
\includegraphics{pr52.png}
\\
Prvo bismo odabrali $k$ različitih stolaca razmišljajući ovako: $S_1$ možemo odabrati na $n$ načina, $S_2$ možemo odabrati na $n-1$ načina, $S_3$ možemo odabrati na $n-2$ načina, i tako sve do $S_k$, kojeg možemo odabrati na $n-k+2$ načina. Kako stolci ipak nisu različiti, svaki odabir stolaca smo brojali više puta. Zato rezultat treba podijeliti s $k! = k \cdot (k-1) \cdot \ldots \cdot 1$, jer se svaki odabir stolaca pojavljuje onoliko puta koliko je različitih poredaka $k$ stolaca. Njih je $k!$ jer prvog možemo odabrati na $k$ načina, drugog na $k-1$, i tako dalje.
\\
Nažalost, u ovom zadatku imam ograničenje: učenici ne mogu sjediti jedan kraj drugog. Kako mu doskočiti? Jedna od prvih ideja koje bi nam mogle pasti napamet je idemo uz stolac blokirati i njegove susjede, dakle postupimo kao u drugom primjeru kada smo braću Grim tretirali kao jedno biće koje sjedi na $2$ stolca. Nažalost, to nije dobro, jer bismo tada u slučaju učenik - prazno - učenik prazninu u sredini blokirali dvaput.
\\
\includegraphics{pr53.png}
\\
Kako ćemo onda doskočiti problemu?
Označimo prvo $k$ stolaca: prvih $k-1$ stolaca bit će nam stolci na koje učenici nikako ne smiju sjesti (stolci između učenika), a zadnji je stolac gdje sjedi zadnji učenik. Između svih oznaka mora postojati razmak osim zadnje.
\\
\includegraphics{pr54.png}
\\
Prvi učenik sjedne neposredno prije prve oznake, drugi neposredno prije druge, ..., dok zadnji sjedne gdje je određeno.
Sada kao u prethodnom primjeru vidimo da je takvih odabira isto koliko zbrojeva
$$x_1+x_2+x_3+...+x_{k-1}+x_k+x_{k+1} = n-k$$
gdje $x_1,...x_{k-1}$ moraju biti pozitivni, a ostala 2 nenegativna ($x$ predstavlja broj sjedala između $2$ oznake, s tim da je $x_{k+1}$ broj sjedala iza zadnje oznake.).
Sada koristimo mali trik kako bismo primijenili formulu izvedenu u prošlom zadatku. Označimo $x_1 = y_1 + 1$, $x_2 = y_2$, $\ldots, x_{k-1} = y_{k-1}$, a zadnja $2$ ostavljamo iste ($y_k = x_k$, $y_{k+1} = x_{k+1}$).
Prikazujući gornju jednadžbu preko varijable $y$ jednadžba postaje:
$$y_1+...+y_{k+1} = n-1$$
gdje su $y_1, \ldots, y_{k+1}$ nenegativni brojevi, što se lako dobije po formuli izvedenom u primjeru $3$.
Kao rješenje upišite "jiayou" (na kineskom: 加油).
 stolaca u istom redu, označenih prirodnim brojevima od
stolaca u istom redu, označenih prirodnim brojevima od  do
do  . Mentori pripremaju učionicu za sastanak tako što stavljaju oznake na stolce na koje će
. Mentori pripremaju učionicu za sastanak tako što stavljaju oznake na stolce na koje će  učenika smjeti sjesti. Koliko ima odabira stolaca ako znamo da učenici ne smiju sjesti jedan do drugoga?
učenika smjeti sjesti. Koliko ima odabira stolaca ako znamo da učenici ne smiju sjesti jedan do drugoga?

 različitih stolaca razmišljajući ovako:
različitih stolaca razmišljajući ovako: 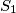 možemo odabrati na
možemo odabrati na  načina,
načina, 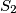 možemo odabrati na
možemo odabrati na  načina,
načina, 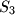 možemo odabrati na
možemo odabrati na  načina, i tako sve do
načina, i tako sve do 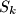 , kojeg možemo odabrati na
, kojeg možemo odabrati na 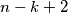 načina. Kako stolci ipak nisu različiti, svaki odabir stolaca smo brojali više puta. Zato rezultat treba podijeliti s
načina. Kako stolci ipak nisu različiti, svaki odabir stolaca smo brojali više puta. Zato rezultat treba podijeliti s 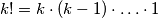 , jer se svaki odabir stolaca pojavljuje onoliko puta koliko je različitih poredaka
, jer se svaki odabir stolaca pojavljuje onoliko puta koliko je različitih poredaka  stolaca. Njih je
stolaca. Njih je 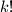 jer prvog možemo odabrati na
jer prvog možemo odabrati na  načina, drugog na
načina, drugog na  , i tako dalje.
, i tako dalje.  stolca. Nažalost, to nije dobro, jer bismo tada u slučaju učenik - prazno - učenik prazninu u sredini blokirali dvaput.
stolca. Nažalost, to nije dobro, jer bismo tada u slučaju učenik - prazno - učenik prazninu u sredini blokirali dvaput. 
 stolaca: prvih
stolaca: prvih  stolaca bit će nam stolci na koje učenici nikako ne smiju sjesti (stolci između učenika), a zadnji je stolac gdje sjedi zadnji učenik. Između svih oznaka mora postojati razmak osim zadnje.
stolaca bit će nam stolci na koje učenici nikako ne smiju sjesti (stolci između učenika), a zadnji je stolac gdje sjedi zadnji učenik. Između svih oznaka mora postojati razmak osim zadnje.
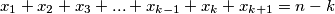 gdje
gdje 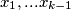 moraju biti pozitivni, a ostala 2 nenegativna (
moraju biti pozitivni, a ostala 2 nenegativna ( predstavlja broj sjedala između
predstavlja broj sjedala između  oznake, s tim da je
oznake, s tim da je 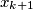 broj sjedala iza zadnje oznake.).
broj sjedala iza zadnje oznake.).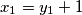 ,
, 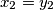 ,
, 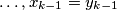 , a zadnja
, a zadnja  ostavljamo iste (
ostavljamo iste (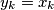 ,
, 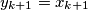 ).
). jednadžba postaje:
jednadžba postaje: 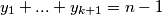 gdje su
gdje su 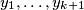 nenegativni brojevi, što se lako dobije po formuli izvedenom u primjeru
nenegativni brojevi, što se lako dobije po formuli izvedenom u primjeru  .
.