Zadatak: Ljepotica i Zvijer organiziraju literarnu večer. Za okrugli stol pozvat će Hansa Christiana Andersena, oba brata Grim, Agathu Christie, Elu Peroci, Matiju Bašića i 3 praščića.
Na koliko načina Ljepotica i Zvijer mogu rasporediti govornike oko okruglog stola ako sva 3 praščića žele sjediti jedan kraj drugog, kao i braća Grim?
Rješenje:

Primijetimo: kad ovaj zadatak ne bi imao uvjet da sva  praščića moraju sjediti skupa, riješili bismo ga kao na predavanju profesorice Zelčić. Naime, prvu osobu mogli bismo posjesti na bilo koje od
praščića moraju sjediti skupa, riješili bismo ga kao na predavanju profesorice Zelčić. Naime, prvu osobu mogli bismo posjesti na bilo koje od  mjesta, iduću na bilo koje od preostalih
mjesta, iduću na bilo koje od preostalih  , i tako dalje. Na kraju bi bilo
, i tako dalje. Na kraju bi bilo  mogućnosti. Primijetimo li još da ćemo svaki poredak dobiti
mogućnosti. Primijetimo li još da ćemo svaki poredak dobiti  puta jer stol možemo rotirati tako da raspored sjedenja ostane isti, dobijamo točno rješenje,
puta jer stol možemo rotirati tako da raspored sjedenja ostane isti, dobijamo točno rješenje, 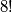 .
.
Kako se sada izboriti s ovim zadatkom?

Kad bismo doživljavali braću Grim kao jednu osobu, te praščiće kao jednu osobu, stol bi imao  mjesta, a mi više ne bismo imali uvjete o sjedenju skupa, pa bismo dobili rješenje
mjesta, a mi više ne bismo imali uvjete o sjedenju skupa, pa bismo dobili rješenje  .
.

Po čemu je naš problem različit od gore riješenog? Pa, za početak, braća Grim mogu sjediti u  moguća poretka, stoga rezultat množimo sa
moguća poretka, stoga rezultat množimo sa  . Praščići pak mogu sjediti u
. Praščići pak mogu sjediti u  mogućih poredaka, pa je konačno rješenje
mogućih poredaka, pa je konačno rješenje  .
.

Kao rješenje upišite "vamos"
\textbf{Zadatak:} Ljepotica i Zvijer organiziraju literarnu večer. Za okrugli stol pozvat će Hansa Christiana Andersena, oba brata Grim, Agathu Christie, Elu Peroci, Matiju Bašića i 3 praščića.
Na koliko načina Ljepotica i Zvijer mogu rasporediti govornike oko okruglog stola ako sva 3 praščića žele sjediti jedan kraj drugog, kao i braća Grim?
\textbf{Rješenje:}
\\
\includegraphics{pr31.png}
\\
Primijetimo: kad ovaj zadatak ne bi imao uvjet da sva $3$ praščića moraju sjediti skupa, riješili bismo ga kao na predavanju profesorice Zelčić. Naime, prvu osobu mogli bismo posjesti na bilo koje od $9$ mjesta, iduću na bilo koje od preostalih $8$, i tako dalje. Na kraju bi bilo $9! = 9 \cdot 8 \cdot \ldots \cdot 1$ mogućnosti. Primijetimo li još da ćemo svaki poredak dobiti $9$ puta jer stol možemo rotirati tako da raspored sjedenja ostane isti, dobijamo točno rješenje, $8!$.
Kako se sada izboriti s ovim zadatkom?
\\
\includegraphics{pr32.png}
\\
Kad bismo doživljavali braću Grim kao jednu osobu, te praščiće kao jednu osobu, stol bi imao $6$ mjesta, a mi više ne bismo imali uvjete o sjedenju skupa, pa bismo dobili rješenje $\frac{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}6 = 5!$.
\\
\includegraphics{pr33.png}
\\
Po čemu je naš problem različit od gore riješenog? Pa, za početak, braća Grim mogu sjediti u $2$ moguća poretka, stoga rezultat množimo sa $2$. Praščići pak mogu sjediti u $3\cdot 2 \cdot 1 = 6$ mogućih poredaka, pa je konačno rješenje $5!\cdot 2 \cdot 6 = 1440$.
\\
\includegraphics{pr34.png}
\\
Kao rješenje upišite "vamos"

 praščića moraju sjediti skupa, riješili bismo ga kao na predavanju profesorice Zelčić. Naime, prvu osobu mogli bismo posjesti na bilo koje od
praščića moraju sjediti skupa, riješili bismo ga kao na predavanju profesorice Zelčić. Naime, prvu osobu mogli bismo posjesti na bilo koje od  mjesta, iduću na bilo koje od preostalih
mjesta, iduću na bilo koje od preostalih  , i tako dalje. Na kraju bi bilo
, i tako dalje. Na kraju bi bilo  mogućnosti. Primijetimo li još da ćemo svaki poredak dobiti
mogućnosti. Primijetimo li još da ćemo svaki poredak dobiti  puta jer stol možemo rotirati tako da raspored sjedenja ostane isti, dobijamo točno rješenje,
puta jer stol možemo rotirati tako da raspored sjedenja ostane isti, dobijamo točno rješenje, 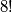 .
.
 mjesta, a mi više ne bismo imali uvjete o sjedenju skupa, pa bismo dobili rješenje
mjesta, a mi više ne bismo imali uvjete o sjedenju skupa, pa bismo dobili rješenje  .
. 
 moguća poretka, stoga rezultat množimo sa
moguća poretka, stoga rezultat množimo sa  . Praščići pak mogu sjediti u
. Praščići pak mogu sjediti u  mogućih poredaka, pa je konačno rješenje
mogućih poredaka, pa je konačno rješenje  .
. 
