Zadatak: . Pauk ima po jednu cipelu i jednu čarapu za svaku od svojih 8 nogu. Na koliko načina se pauk može obuti ako na svaku nogu najprije mora obući čarapu, a onda cipelu. Prebrojavamo procese oblačenja, a ne konačan rezultat!
Rješenje: Dobra strategija za započeti zadatak je uvijek zapitati se što mi se to u njemu ne sviđa. Ovdje je to uvjet da se čarapa uvijek mora obući prije cipele. Kako bih riješila zadatak bez toga?
Pa jednostavno! Imam 16 mogućih komada obuće. Prvi komad obuće mogu staviti na koje god želim mjesto, drugi bilo gdje gdje nije prvi, treći bilo gdje gdje nisu prvi i drugi... Takvim razmišljanjem dođem do rezultata 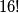 .
.
Sada si moram postaviti  pitanja:
pitanja:
1. Jesam li sve procese koji su u rješenju brojala bar jedanput? Jesam.
2. Jesam li neke procese brojala više puta ili brojala procese koje ne bih smjela? Nažalost jesam - ignorirala sam uvjet da pauk uvijek prvo oblači čarapu pa cipelu. Tako sam primjerice brojala proces u kojem pauk prvo obuče sve cipele, a tek zatim sve čarape.
Koliko sam takvih procesa prebrojala?
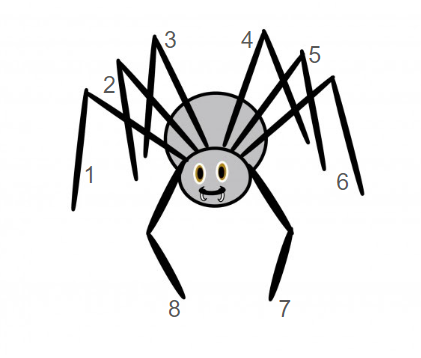
Kako bih lakše razmišljala o tome, svakom ću procesu pridružiti kod. Označit ću paukove noge brojevima od 1 do 8, te ću svaki korak zapisati kao  (ča) ako je na
(ča) ako je na  tu nogu obukao čarapu, a
tu nogu obukao čarapu, a  (ci) ako je na
(ci) ako je na  (tu) nogu obukao cipelu.
(tu) nogu obukao cipelu.
Primjerice, procesu u kojem pauk prvo na noge od 1 do 8 obuče čarape, a onda na noge od 8 do 1 cipele pridružila bih kod
1(ča) 2(ča) 3(ča) 4(ča) 5(ča) 6(ča) 7(ča) 8(ča) 8(ci) 7(ci) 6(ci) 5(ci) 4(ci) 3(ci) 2(ci) 1(ci)
Promotrimo neki nevaljani kod, primjerice:
1(ča) 2(ča) 3(ča) 4(ci) 5(ča) 6(ča) 7(ča) 8(ča) 8(ci) 7(ci) 6(ci) 5(ci) 4(ča) 3(ci) 2(ci) 1(ci)
Zašto je nevaljan? Zato što pauk na četvrtu nogu prvo stavi cipelu, zatim čarapu.
Znam li neki način za pretvoriti ga u valjani kod? Jednostavno, svugdje gdje se  (ci) pojavljuje prije
(ci) pojavljuje prije  (ča) zamijenim im mjesta. Tako gornji kod postaje valjani
(ča) zamijenim im mjesta. Tako gornji kod postaje valjani
1(ča) 2(ča) 3(ča) 4(ča) 5(ča) 6(ča) 7(ča) 8(ča) 8(ci) 7(ci) 6(ci) 5(ci) 4(ci) 3(ci) 2(ci) 1(ci)
Na taj način svaki nevaljani kod na jedinstven način mogu pretvoriti u valjani. Koliko nevaljanih kodova pridružujemo isti valjani kod?
1( ) 2( ) 3( ) 4( ) 5( ) 6( ) 7( ) 8( ) 8( ) 7( ) 6( ) 5( ) 4( ) 3( ) 2( ) 1( )
Poredak brojeva mi mora biti isti kod nevaljanih kodova i valjanog kojeg im pridružujem. Zatim za svaku nogu na  načina biramo hoćemo li prvo staviti cipelu ili čarapu. Kako je nogu
načina biramo hoćemo li prvo staviti cipelu ili čarapu. Kako je nogu  , odabira je
, odabira je 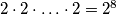 , a samo jedan je valjan, onaj u kojem smo na svaku nogu prvo stavili čarapu.
, a samo jedan je valjan, onaj u kojem smo na svaku nogu prvo stavili čarapu.
To znači da smo 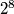 kodova pridružili isti kod, od kojih je samo jedan valjan. Dakle, rješenje ću dobiti ako
kodova pridružili isti kod, od kojih je samo jedan valjan. Dakle, rješenje ću dobiti ako 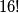 podijelim sa
podijelim sa 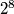 , pa je to
, pa je to 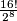 .
.
Kao rješenje upišite "yay".
\textbf{Zadatak:} . Pauk ima po jednu cipelu i jednu čarapu za svaku od svojih 8 nogu. Na koliko načina se pauk
može obuti ako na svaku nogu najprije mora obući čarapu, a onda cipelu. Prebrojavamo procese oblačenja, a
ne konačan rezultat!
\textbf{Rješenje:}
Dobra strategija za započeti zadatak je uvijek zapitati se što mi se to u njemu \emph{ne} sviđa. Ovdje je to uvjet da se čarapa uvijek mora obući prije cipele. Kako bih riješila zadatak bez toga?
Pa jednostavno! Imam 16 mogućih komada obuće. Prvi komad obuće mogu staviti na koje god želim mjesto, drugi bilo gdje gdje nije prvi, treći bilo gdje gdje nisu prvi i drugi... Takvim razmišljanjem dođem do rezultata $16!$.
Sada si moram postaviti $2$ pitanja:
1. Jesam li sve procese koji su u rješenju brojala bar jedanput? Jesam.
2. Jesam li neke procese brojala više puta ili brojala procese koje ne bih smjela? Nažalost jesam - ignorirala sam uvjet da pauk uvijek prvo oblači čarapu pa cipelu. Tako sam primjerice brojala proces u kojem pauk prvo obuče sve cipele, a tek zatim sve čarape.
Koliko sam takvih procesa prebrojala?
Kako bih lakše razmišljala o tome, svakom ću procesu pridružiti kod. Označit ću paukove noge brojevima od 1 do 8, te ću svaki korak zapisati kao $n$(ča) ako je na $n$tu nogu obukao čarapu, a $n$(ci) ako je na $n$(tu) nogu obukao cipelu.
\\
\includegraphics{pr21.png}
\\
Primjerice, procesu u kojem pauk prvo na noge od 1 do 8 obuče čarape, a onda na noge od 8 do 1 cipele pridružila bih kod \\
1(ča) 2(ča) 3(ča) 4(ča) 5(ča) 6(ča) 7(ča) 8(ča) 8(ci) 7(ci) 6(ci) 5(ci) 4(ci) 3(ci) 2(ci) 1(ci) \\
Promotrimo neki nevaljani kod, primjerice:\\
1(ča) 2(ča) 3(ča) 4(ci) 5(ča) 6(ča) 7(ča) 8(ča) 8(ci) 7(ci) 6(ci) 5(ci) 4(ča) 3(ci) 2(ci) 1(ci) \\
Zašto je nevaljan? Zato što pauk na četvrtu nogu prvo stavi cipelu, zatim čarapu. \\
Znam li neki način za pretvoriti ga u valjani kod? Jednostavno, svugdje gdje se $n$(ci) pojavljuje prije $n$(ča) zamijenim im mjesta. Tako gornji kod postaje valjani \\
1(ča) 2(ča) 3(ča) 4(ča) 5(ča) 6(ča) 7(ča) 8(ča) 8(ci) 7(ci) 6(ci) 5(ci) 4(ci) 3(ci) 2(ci) 1(ci) \\
Na taj način svaki nevaljani kod na jedinstven način mogu pretvoriti u valjani. Koliko nevaljanih kodova pridružujemo isti valjani kod? \\
1( ) 2( ) 3( ) 4( ) 5( ) 6( ) 7( ) 8( ) 8( ) 7( ) 6( ) 5( ) 4( ) 3( ) 2( ) 1( ) \\
Poredak brojeva mi mora biti isti kod nevaljanih kodova i valjanog kojeg im pridružujem. Zatim za svaku nogu na $2$ načina biramo hoćemo li prvo staviti cipelu ili čarapu. Kako je nogu $8$, odabira je $2\cdot 2 \cdot \ldots \cdot 2 = 2^8$, a samo jedan je valjan, onaj u kojem smo na svaku nogu prvo stavili čarapu.
To znači da smo $2^8$ kodova pridružili isti kod, od kojih je samo jedan valjan. Dakle, rješenje ću dobiti ako $16!$ podijelim sa $2^8$, pa je to $\frac{16!}{2^8}$.
Kao rješenje upišite "yay".
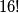 .
. pitanja:
pitanja: (ča) ako je na
(ča) ako je na  tu nogu obukao čarapu, a
tu nogu obukao čarapu, a  (ci) ako je na
(ci) ako je na  (tu) nogu obukao cipelu.
(tu) nogu obukao cipelu.
 (ci) pojavljuje prije
(ci) pojavljuje prije  (ča) zamijenim im mjesta. Tako gornji kod postaje valjani
(ča) zamijenim im mjesta. Tako gornji kod postaje valjani  načina biramo hoćemo li prvo staviti cipelu ili čarapu. Kako je nogu
načina biramo hoćemo li prvo staviti cipelu ili čarapu. Kako je nogu  , odabira je
, odabira je 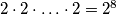 , a samo jedan je valjan, onaj u kojem smo na svaku nogu prvo stavili čarapu.
, a samo jedan je valjan, onaj u kojem smo na svaku nogu prvo stavili čarapu.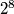 kodova pridružili isti kod, od kojih je samo jedan valjan. Dakle, rješenje ću dobiti ako
kodova pridružili isti kod, od kojih je samo jedan valjan. Dakle, rješenje ću dobiti ako 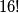 podijelim sa
podijelim sa 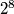 , pa je to
, pa je to 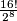 .
.