Dragi učenici, dobrodošli u 4. tjedan MetaMath tečaja!
Ovaj tjedan bavit ćemo se zadacima s prebrojavanjima. S obzirom da ovo čitate, vjerujem da ste videolekciju koju je za vas pripremila profesorica Zelčić već pogledali. Ja se na nju planiram tek nadovezati s nekoliko primjera, a na kraju ovog lanca čeka vas i kreativni zadatak.
Za dodatne zadatke svakako bacite oko na ovo odlično raspisano MNM predavanje o prebrojavanjima. Prirodni nastavak ove teme bila bi dvostruka prebrojavanja o kojima možete više vidjeti na linku, a za čitatelje koji sanjare o avionskim kartama na HMDov račun toplo preporučujem ovo odlično predavanje s MEMO priprema profesora Ilka Brnetića.
Ako netko pak voli teoriju i traži svoj idući matematički projektić (možda za prijaviti na MNM matematičku konferenciju ovo ljeto?), može baciti oko na skriptu iz kolegija Diskretna matematika na PMFu - gradivo je jako zanimljivo, a skripta je poprilično čitljiva. Ako mu se svidi to što vidi može čak i pogledati snimke predavanja profesorice Marcele Hanzer iz COVIDa na Meduzi.
Preporuka za dokone olimpijce: Od naprednog faksovskog gradiva koje bi vam moglo unaprijediti olimpijske karijere iz ovog dijela ističem funkcije izvodnice. To vam je nešto kao trig bash u geometriji, ali za kombe. Ima malo posla dok se to ne nauči, ali kasnije možete na jednostavniji način riješiti puno teških kombi. Ako ste zainteresirani pogledajte skriptu iz vježbi.
Tako, sad kad ste oboružani raznim materijalima, krenimo na posao!
Zadatak: Na koliko se načina sva slova A B C D E F G H I mogu poredati tako da su i samoglasnici i suglasnici poredani abecednim redom?
Rješenje:
Aha, zadatak mi zapravo kaže da će mi se samoglasnici uvijek pojaviti u redoslijedu A E I, a suglasnici uvijek u redoslijedu B C D F G H. . Za mene je to odlično - ako znam na kojim mjestima u riječi dolaze samoglasnici, znam i cijelu riječ!

Na koliko načina mogu odabrati mjesta za samoglasnike u riječi od 9 slova?
Pa, prvo mjesto može biti bilo koje, pa za njega imam 9 mogućnosti. Drugo može biti bilo koje osim već odabranog, pa za njega imam 8 mogućnosti. Analogno, za treće imam 7. No redoslijed odabira mjesta u ovom mi zadatku ne igra ulogu (samoglasnici uvijek idu redom A E I), stoga moram podijeliti s brojem poredaka slova A E I, a to je 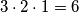 . Rješenje je stoga
. Rješenje je stoga 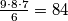 .
.
Za detaljnije objašnjenje ovog postupka pogledajte već spomenuti video profesorice Zelčić.
Kao rješenje upišite riječ koju dobijete ako znate da u narančaste kućice sa slike idu samoglasnici.
Dragi učenici, dobrodošli u 4. tjedan MetaMath tečaja!
Ovaj tjedan bavit ćemo se zadacima s prebrojavanjima. S obzirom da ovo čitate, vjerujem da ste \href{https://www.youtube.com/watch?v=EZO8oobkzY8}{videolekciju} koju je za vas pripremila profesorica Zelčić već pogledali. Ja se na nju planiram tek nadovezati s nekoliko primjera, a na kraju ovog lanca čeka vas i kreativni zadatak.
Za dodatne zadatke svakako bacite oko na \href{https://umo.mathos.unios.hr/wp-content/uploads/2022/12/Osijek_2022_2023__J4.pdf}{ovo odlično raspisano MNM predavanje o prebrojavanjima}. Prirodni nastavak ove teme bila bi \href{https://natjecanja.math.hr/wp-content/uploads/2016/12/Prebrojavanje-i-dvostruko-prebrojavanje-Azra-Tafro.pdf}{dvostruka prebrojavanja} o kojima možete više vidjeti na linku,
a za čitatelje koji sanjare o avionskim kartama na HMDov račun toplo preporučujem ovo \href{https://natjecanja.math.hr/wp-content/uploads/2015/08/C-Prebrojavanje-Ilko-Brnetic.pdf}{odlično predavanje s MEMO priprema profesora Ilka Brnetića}.
Ako netko pak voli teoriju i traži svoj idući matematički projektić (možda za prijaviti na MNM matematičku konferenciju ovo ljeto?), može baciti oko na \href{https://web.math.pmf.unizg.hr/nastava/komb/predavanja/predavanja.pdf}{skriptu} iz kolegija Diskretna matematika na PMFu - gradivo je jako zanimljivo, a skripta je poprilično čitljiva. Ako mu se svidi to što vidi može čak i pogledati snimke predavanja profesorice Marcele Hanzer iz COVIDa \href{https://meduza.carnet.hr/index.php/media/videos?pack=882}{na Meduzi}.
\\ Preporuka za dokone olimpijce: Od naprednog faksovskog gradiva koje bi vam moglo unaprijediti olimpijske karijere iz ovog dijela ističem funkcije izvodnice. To vam je nešto kao trig bash u geometriji, ali za kombe. Ima malo posla dok se to ne nauči, ali kasnije možete na jednostavniji način riješiti puno teških kombi. Ako ste zainteresirani pogledajte \href{https://web.math.pmf.unizg.hr/~ikrijan/pdfs/nastava/diskretna.pdf}{skriptu iz vježbi}. \\\\
Tako, sad kad ste oboružani raznim materijalima, krenimo na posao! \\\\\\
\textbf{Zadatak:}
Na koliko se načina sva slova A B C D E F G H I mogu poredati tako da su i samoglasnici i suglasnici
poredani abecednim redom?
\\
\textbf{Rješenje:}
\\
Aha, zadatak mi zapravo kaže da će mi se samoglasnici uvijek pojaviti u redoslijedu A E I, a suglasnici uvijek u redoslijedu B C D F G H. .
Za mene je to odlično - ako znam na kojim mjestima u riječi dolaze samoglasnici, znam i cijelu riječ!
\\
\includegraphics{pr11.png}
\\
Na koliko načina mogu odabrati mjesta za samoglasnike u riječi od 9 slova?
Pa, prvo mjesto može biti bilo koje, pa za njega imam 9 mogućnosti. Drugo može biti bilo koje osim već odabranog, pa za njega imam 8 mogućnosti. Analogno, za treće imam 7. No redoslijed odabira mjesta u ovom mi zadatku ne igra ulogu (samoglasnici uvijek idu redom A E I), stoga moram podijeliti s brojem poredaka slova A E I, a to je $3 \cdot 2 \cdot 1 = 6$. Rješenje je stoga $\frac{9\cdot 8 \cdot 7}{6} = 84$.
Za detaljnije objašnjenje ovog postupka pogledajte već spomenuti video profesorice Zelčić.
Kao rješenje upišite riječ koju dobijete ako znate da u narančaste kućice sa slike idu samoglasnici.

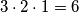 . Rješenje je stoga
. Rješenje je stoga 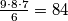 .
.