Dobro došli u 6. tjedan MetaMath tečaja. Ovaj tjedan se bavimo s jednim malo specifičnijim područjem algebre. U školi se od 1. razreda počinje s prirodnim brojevima, 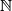 , onda se i uvede minus pa dobijemo cijele brojeve,
, onda se i uvede minus pa dobijemo cijele brojeve, 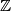 te dijeljenjem racionalni,
te dijeljenjem racionalni, 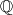 . Tada neko vrijeme nema novih brojeva.
. Tada neko vrijeme nema novih brojeva.
No, u nekom trenutku se uvedu i realni brojevi, koji nam i trebaju u geometriji te vrlo često u kvadratnim jednadžbama, poput 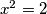 gdje dobijemo rješenja
gdje dobijemo rješenja 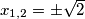 .
.
Mogli bismo se zapitati je li nam to dovoljno. Primjerice, ako broj pomnožimo sa samim sobom uvijek dobijemo nešto pozitivno jer se minusi "ponište", ali stoga jednadžba poput 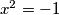 nema rješenje nad realnim brojevima i opet nam treba nešto više brojeva. Sada se postavlja pitanje - možemo li to dalje proširiti te kako? Odgovor je da, naime, i tako dolazimo do teme predavanja - kompleksnih brojeva,
nema rješenje nad realnim brojevima i opet nam treba nešto više brojeva. Sada se postavlja pitanje - možemo li to dalje proširiti te kako? Odgovor je da, naime, i tako dolazimo do teme predavanja - kompleksnih brojeva, 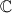 . Kompleksni brojevi se temelje na rješenju jednadžbe
. Kompleksni brojevi se temelje na rješenju jednadžbe 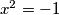 gdje definiramo imaginarnu jedinicu
gdje definiramo imaginarnu jedinicu  kao
kao 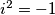 .
.
Dakle, što jesu točno kompleksni brojevi? To su svi brojevi  oblika
oblika 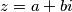 gdje su
gdje su 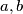 neki realni brojevi. Vidimo da imamo dio bez
neki realni brojevi. Vidimo da imamo dio bez  koji ćemo nazivati realni dio te dio uz
koji ćemo nazivati realni dio te dio uz  koji ćemo zvati imaginarni dio. U oznakama će to biti
koji ćemo zvati imaginarni dio. U oznakama će to biti 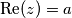 (ili više fancy
(ili više fancy 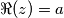 ) za realni te
) za realni te 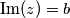 (ili više fancy
(ili više fancy 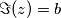 ) za imaginarni, primijetite da imaginarni dio pišemo bez
) za imaginarni, primijetite da imaginarni dio pišemo bez  .
.
U ovom PDF-u se nalazi uvodna teorija, riješeni primjeri i svi zadaci
Za dobivanje boda kao rješenje upišite zbroj kvadrata najmanjeg prirodnog broja i najvećeg parnog prostog broja.
Dobro došli u 6. tjedan MetaMath tečaja. Ovaj tjedan se bavimo s jednim malo specifičnijim područjem algebre. U školi se od 1. razreda počinje s prirodnim brojevima, $\mathbb{N}$, onda se i uvede minus pa dobijemo cijele brojeve, $\mathbb{Z}$ te dijeljenjem racionalni, $\mathbb{Q}$. Tada neko vrijeme nema novih brojeva.
No, u nekom trenutku se uvedu i realni brojevi, koji nam i trebaju u geometriji te vrlo često u kvadratnim jednadžbama, poput $x^2=2$ gdje dobijemo rješenja $x_{1,2}=\pm\sqrt{2}$.
Mogli bismo se zapitati je li nam to dovoljno. Primjerice, ako broj pomnožimo sa samim sobom uvijek dobijemo nešto pozitivno jer se minusi "ponište", ali stoga jednadžba poput $x^2=-1$ nema rješenje nad realnim brojevima i opet nam treba nešto više brojeva. Sada se postavlja pitanje - možemo li to dalje proširiti te kako? Odgovor je da, naime, i tako dolazimo do teme predavanja - \textbf{kompleksnih brojeva}, $\mathbb{C}$. Kompleksni brojevi se temelje na rješenju jednadžbe $x^2=-1$ gdje definiramo \textbf{imaginarnu jedinicu} $i$ kao $i^2=-1$.
Dakle, što jesu točno kompleksni brojevi? To su svi brojevi $z$ oblika $z=a+bi$ gdje su $a,b$ neki realni brojevi. Vidimo da imamo dio bez $i$ koji ćemo nazivati \textbf{realni dio} te dio uz $i$
koji ćemo zvati \textbf{imaginarni dio}. U oznakama će to biti $\text{Re}(z)=a$ (ili više fancy $\Re(z)=a$) za realni te $\text{Im}(z)=b$ (ili više fancy $\Im(z)=b$) za imaginarni, primijetite da imaginarni dio pišemo bez $i$.
U \href{https://drive.google.com/file/d/1VrWfvDnOeQh_FYoW8NIx_KCEX-7UrofV/view?usp=sharing}{ovom PDF-u} se nalazi uvodna teorija, riješeni primjeri i svi zadaci
Za dobivanje boda kao rješenje upišite zbroj kvadrata najmanjeg prirodnog broja i najvećeg parnog prostog broja.
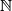 , onda se i uvede minus pa dobijemo cijele brojeve,
, onda se i uvede minus pa dobijemo cijele brojeve, 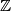 te dijeljenjem racionalni,
te dijeljenjem racionalni, 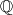 . Tada neko vrijeme nema novih brojeva.
. Tada neko vrijeme nema novih brojeva.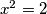 gdje dobijemo rješenja
gdje dobijemo rješenja 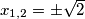 .
.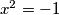 nema rješenje nad realnim brojevima i opet nam treba nešto više brojeva. Sada se postavlja pitanje - možemo li to dalje proširiti te kako? Odgovor je da, naime, i tako dolazimo do teme predavanja - kompleksnih brojeva,
nema rješenje nad realnim brojevima i opet nam treba nešto više brojeva. Sada se postavlja pitanje - možemo li to dalje proširiti te kako? Odgovor je da, naime, i tako dolazimo do teme predavanja - kompleksnih brojeva, 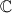 . Kompleksni brojevi se temelje na rješenju jednadžbe
. Kompleksni brojevi se temelje na rješenju jednadžbe 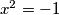 gdje definiramo imaginarnu jedinicu
gdje definiramo imaginarnu jedinicu  kao
kao 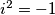 .
. oblika
oblika 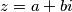 gdje su
gdje su 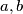 neki realni brojevi. Vidimo da imamo dio bez
neki realni brojevi. Vidimo da imamo dio bez  koji ćemo nazivati realni dio te dio uz
koji ćemo nazivati realni dio te dio uz  koji ćemo zvati imaginarni dio. U oznakama će to biti
koji ćemo zvati imaginarni dio. U oznakama će to biti 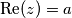 (ili više fancy
(ili više fancy 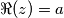 ) za realni te
) za realni te 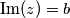 (ili više fancy
(ili više fancy 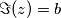 ) za imaginarni, primijetite da imaginarni dio pišemo bez
) za imaginarni, primijetite da imaginarni dio pišemo bez  .
.