Tako dolazimo do prvog zadatka gdje ćemo se upoznat s nekim od novih pojmova:
Primjer. 1. U skupu kompleksnih brojeva riješite jednadžbu 
Rješenje. Dakle, počnimo s malim pojednostavljenjem, kao što smo vidjeli potencija broja  se ponavljaju nakon svake 4 pa kako je
se ponavljaju nakon svake 4 pa kako je  imamo
imamo  Jednadžba postaje
Jednadžba postaje  Sada da smo nad realnim brojevima bi grupirali sve sa
Sada da smo nad realnim brojevima bi grupirali sve sa  zajedno i podijelili, ali ovdje imamo
zajedno i podijelili, ali ovdje imamo  i
i 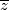 pa ne možemo direktno dobiti
pa ne možemo direktno dobiti  , ali zato imamo jednu drugu metodu, možemo rastaviti
, ali zato imamo jednu drugu metodu, možemo rastaviti  na realni i imaginarni dio
na realni i imaginarni dio 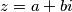 te kada to uvrstimo dobijemo
te kada to uvrstimo dobijemo  Sada dolazimo do onog lijepog dijela, možemo gledati realni i imaginarni dio zasebno, tj. mi u jednoj jednadžbi zapravo imamo sustav jednadžbi jer možemo zasebno promatrati jednakost brojeva bez
Sada dolazimo do onog lijepog dijela, možemo gledati realni i imaginarni dio zasebno, tj. mi u jednoj jednadžbi zapravo imamo sustav jednadžbi jer možemo zasebno promatrati jednakost brojeva bez  i jednakost brojeva s
i jednakost brojeva s  , stoga isčitavamo sustav (za jednakost imaginarnih dijelova možemo i maknuti
, stoga isčitavamo sustav (za jednakost imaginarnih dijelova možemo i maknuti  jer bi ga svi elementi u jednadžbi imali)
jer bi ga svi elementi u jednadžbi imali)  možemo pomnožiti drugu jednadžbu s
možemo pomnožiti drugu jednadžbu s  te zbrojiti (da nam se pokrate članovi s
te zbrojiti (da nam se pokrate članovi s  ) ih da bismo dobili
) ih da bismo dobili  , tj.
, tj.  te kada uvrstimo natrag u drugu jednadžbu
te kada uvrstimo natrag u drugu jednadžbu  , tj.
, tj.  . No, nismo gotovi još jer nas ne traži zapravo uređene parove
. No, nismo gotovi još jer nas ne traži zapravo uređene parove 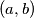 nego je to samo oznaka koju smo si uveli. Zadatak nas traži kompleksne brojeve
nego je to samo oznaka koju smo si uveli. Zadatak nas traži kompleksne brojeve 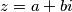 , što je u našem slučaju samo jedno rješenje
, što je u našem slučaju samo jedno rješenje  .
.
Kako biste dobili bod upišite 1 kao rješenje.
Tako dolazimo do prvog zadatka gdje ćemo se upoznat s nekim od novih pojmova:
\textit{Primjer. 1.} U skupu kompleksnih brojeva riješite jednadžbu
$$z(4+i)+\overline{z}(2-3i)=1-i^{11}$$
\textit{Rješenje.} Dakle, počnimo s malim pojednostavljenjem, kao što smo vidjeli potencija broja $i$ se ponavljaju nakon svake 4 pa kako je $11=4\cdot2+3$ imamo $$i^{11}=i^{2\cdot4}\cdot i^3=(\underbrace{i^4}_{1})^2\cdot(\underbrace{i^2}_{-1}\cdot i)=-i$$
Jednadžba postaje $$z(4+i)+\overline{z}(2-3i)=1+i$$
Sada da smo nad realnim brojevima bi grupirali sve sa $z$ zajedno i podijelili, ali ovdje imamo $z$ i $\overline{z}$ pa ne možemo direktno dobiti $z=\text{broj}$, ali zato imamo jednu drugu metodu, možemo rastaviti $z$ na realni i imaginarni dio $z=a+bi$ te kada to uvrstimo dobijemo
\begin{align*}
(a+bi)(4+i)+(a-bi)(2-3i)&=1+i\\
4a+ai+4bi+\underbrace{bi^2}_{-b}+2a-3ai-2bi+\underbrace{3bi^2}_{-3b}&=1+i\\
6a-4b-2ai+2bi&=1+i\\
\end{align*}
Sada dolazimo do onog lijepog dijela, možemo gledati realni i imaginarni dio zasebno, tj. mi u jednoj jednadžbi zapravo imamo sustav jednadžbi jer možemo zasebno promatrati jednakost brojeva bez $i$ i jednakost brojeva s $i$, stoga isčitavamo sustav (za jednakost imaginarnih dijelova možemo i maknuti $i$ jer bi ga svi elementi u jednadžbi imali)
\begin{align*}
6a-4b&=1\\
-2a+2b&=1
\end{align*}
možemo pomnožiti drugu jednadžbu s $2$ te zbrojiti (da nam se pokrate članovi s $b$) ih da bismo dobili $2a=3$, tj. $a=\frac{3}{2}$ te kada uvrstimo natrag u drugu jednadžbu $2b=1+2a$, tj. $b=2$. No, nismo gotovi još jer nas ne traži zapravo uređene parove $(a,b)$ nego je to samo oznaka koju smo si uveli. Zadatak nas traži kompleksne brojeve $z=a+bi$, što je u našem slučaju samo jedno rješenje $z=\frac{3}{2}+2i$.
Kako biste dobili bod upišite 1 kao rješenje.

 se ponavljaju nakon svake 4 pa kako je
se ponavljaju nakon svake 4 pa kako je  imamo
imamo  Jednadžba postaje
Jednadžba postaje  Sada da smo nad realnim brojevima bi grupirali sve sa
Sada da smo nad realnim brojevima bi grupirali sve sa  zajedno i podijelili, ali ovdje imamo
zajedno i podijelili, ali ovdje imamo  i
i 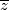 pa ne možemo direktno dobiti
pa ne možemo direktno dobiti  , ali zato imamo jednu drugu metodu, možemo rastaviti
, ali zato imamo jednu drugu metodu, možemo rastaviti  na realni i imaginarni dio
na realni i imaginarni dio 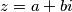 te kada to uvrstimo dobijemo
te kada to uvrstimo dobijemo  Sada dolazimo do onog lijepog dijela, možemo gledati realni i imaginarni dio zasebno, tj. mi u jednoj jednadžbi zapravo imamo sustav jednadžbi jer možemo zasebno promatrati jednakost brojeva bez
Sada dolazimo do onog lijepog dijela, možemo gledati realni i imaginarni dio zasebno, tj. mi u jednoj jednadžbi zapravo imamo sustav jednadžbi jer možemo zasebno promatrati jednakost brojeva bez  i jednakost brojeva s
i jednakost brojeva s  , stoga isčitavamo sustav (za jednakost imaginarnih dijelova možemo i maknuti
, stoga isčitavamo sustav (za jednakost imaginarnih dijelova možemo i maknuti  jer bi ga svi elementi u jednadžbi imali)
jer bi ga svi elementi u jednadžbi imali)  možemo pomnožiti drugu jednadžbu s
možemo pomnožiti drugu jednadžbu s  te zbrojiti (da nam se pokrate članovi s
te zbrojiti (da nam se pokrate članovi s  ) ih da bismo dobili
) ih da bismo dobili  , tj.
, tj.  te kada uvrstimo natrag u drugu jednadžbu
te kada uvrstimo natrag u drugu jednadžbu  , tj.
, tj.  . No, nismo gotovi još jer nas ne traži zapravo uređene parove
. No, nismo gotovi još jer nas ne traži zapravo uređene parove 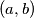 nego je to samo oznaka koju smo si uveli. Zadatak nas traži kompleksne brojeve
nego je to samo oznaka koju smo si uveli. Zadatak nas traži kompleksne brojeve 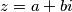 , što je u našem slučaju samo jedno rješenje
, što je u našem slučaju samo jedno rješenje  .
.