Makar smo vidjeli da nam uvođenje 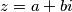 može pomoći, ponekad nam može i jako zakomplicirati život. Tako je općenito u matematici - metoda ili trik za riješiti jedan problem ne mora nužno pomoć na drugom, štoviše može i odmoć.
može pomoći, ponekad nam može i jako zakomplicirati život. Tako je općenito u matematici - metoda ili trik za riješiti jedan problem ne mora nužno pomoć na drugom, štoviše može i odmoć.
Primjer. 2. Odredite sve kompleksne brojeve  takve da je
takve da je 
Rješenje. Za prvi način ćemo probat opet isto, neka nam je 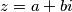 i pokušajmo odrediti
i pokušajmo odrediti 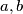 . No, u broju
. No, u broju  ne možemo odmah isčitati koji je realni a koji je imaginarni dio i zbog ovoga ćemo se napatit ovim načinom. Problem nam stvara što je
ne možemo odmah isčitati koji je realni a koji je imaginarni dio i zbog ovoga ćemo se napatit ovim načinom. Problem nam stvara što je  u nazivniku, ali ne pretjerani problem - može nam poslužiti jedna od tvrdnji iz uvoda. Želimo imati realan broj u nazivniku, a znamo da je
u nazivniku, ali ne pretjerani problem - može nam poslužiti jedna od tvrdnji iz uvoda. Želimo imati realan broj u nazivniku, a znamo da je  uvijek realan, tako da broj
uvijek realan, tako da broj  možemo uvijek proširiti sa
možemo uvijek proširiti sa  kako bismo mogli isčitati realni i imaginarni dio, ovdje nam treba
kako bismo mogli isčitati realni i imaginarni dio, ovdje nam treba 

Sada bi nam preostao sustav  koji možete slobodno pokušati riješiti za vježbu. No, postoji bolji način za to riješiti.
koji možete slobodno pokušati riješiti za vježbu. No, postoji bolji način za to riješiti.
 je neki kompleksni broj
je neki kompleksni broj  , a svaki se može zapisati kao
, a svaki se može zapisati kao  , a mi znamo
, a mi znamo  te kada to uvrstimo imamo jednadžbu
te kada to uvrstimo imamo jednadžbu  koju rješavamo slično kao da imamo
koju rješavamo slično kao da imamo  u realnima, tako da sve invertiramo, tj. zamjenimo svemu brojnik i nazivnik te dalje možemo direktno dobiti
u realnima, tako da sve invertiramo, tj. zamjenimo svemu brojnik i nazivnik te dalje možemo direktno dobiti  za razliku od prvog primjera.
za razliku od prvog primjera. 
Kako biste dobili bod na ovom zadatku, upišite 2 kao rješenje.
Makar smo vidjeli da nam uvođenje $z=a+bi$ može pomoći, ponekad nam može i jako zakomplicirati život. Tako je općenito u matematici - metoda ili trik za riješiti jedan problem ne mora nužno pomoć na drugom, štoviše može i odmoć.
\textit{Primjer. 2.} Odredite sve kompleksne brojeve $z$ takve da je
$$\text{Re}\frac{1}{1-z}=2\quad\text{i}\quad\text{Im}\frac{1}{1-z}=-1$$
\textit{Rješenje.} Za prvi način ćemo probat opet isto, neka nam je $z=a+bi$ i pokušajmo odrediti $a,b$. No, u broju $\dfrac{1}{1-a-bi}$ ne možemo odmah isčitati koji je realni a koji je imaginarni dio i zbog ovoga ćemo se napatit ovim načinom. Problem nam stvara što je $i$ u nazivniku, ali ne pretjerani problem - može nam poslužiti jedna od tvrdnji iz uvoda. Želimo imati realan broj u nazivniku, a znamo da je $\lvert z\rvert$ uvijek realan, tako da broj $\frac{1}{z}$ možemo uvijek proširiti sa $\overline{z}$ kako bismo mogli isčitati realni i imaginarni dio, ovdje nam treba $\overline{1-a-bi}=1-a+bi$
$$\frac{1}{1-z}=\frac{1}{1-a-bi}\cdot\frac{\overline{1-a-bi}}{\overline{1-a-bi}}
\frac{1-a+bi}{\lvert1-a-bi\rvert^2}=\frac{1-a+bi}{(1-a)^2+b^2}$$
Sada bi nam preostao sustav
\begin{align*}
\frac{1-a}{(1-a)^2+b^2}=2,\quad\frac{b}{(1-a)^2+b^2}=-1
\end{align*}
koji možete slobodno pokušati riješiti za vježbu. No, postoji bolji način za to riješiti.
$\dfrac{1}{1-z}$ je neki kompleksni broj $w$, a svaki se može zapisati kao $w=\text{Re}(w)+\text{Im}(w)\cdot i$, a mi znamo $\text{Re}(w),\text{Im}(w)$ te kada to uvrstimo imamo jednadžbu
$$\frac{1}{1-z}=2-i$$
koju rješavamo slično kao da imamo $\frac{1}{x}=\text{broj}$ u realnima, tako da sve invertiramo, tj. zamjenimo svemu brojnik i nazivnik te dalje možemo direktno dobiti $z$ za razliku od prvog primjera.
\begin{align*}
1-z=\frac{1}{2-i}\cdot\frac{\overline{2-i}}{\overline{2-i}}&=\frac{2+i}{\lvert2+i\rvert}=\frac{2+i}{2^2+1^2}\\
1-z&=\frac{2}{5}+\frac{1}{5}i\\
-z&=-\frac{3}{5}+\frac{1}{5}i\\
z&=\frac{3}{5}-\frac{1}{5}i
\end{align*}
Kako biste dobili bod na ovom zadatku, upišite 2 kao rješenje.
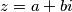 može pomoći, ponekad nam može i jako zakomplicirati život. Tako je općenito u matematici - metoda ili trik za riješiti jedan problem ne mora nužno pomoć na drugom, štoviše može i odmoć.
može pomoći, ponekad nam može i jako zakomplicirati život. Tako je općenito u matematici - metoda ili trik za riješiti jedan problem ne mora nužno pomoć na drugom, štoviše može i odmoć. takve da je
takve da je 
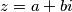 i pokušajmo odrediti
i pokušajmo odrediti 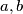 . No, u broju
. No, u broju  ne možemo odmah isčitati koji je realni a koji je imaginarni dio i zbog ovoga ćemo se napatit ovim načinom. Problem nam stvara što je
ne možemo odmah isčitati koji je realni a koji je imaginarni dio i zbog ovoga ćemo se napatit ovim načinom. Problem nam stvara što je  u nazivniku, ali ne pretjerani problem - može nam poslužiti jedna od tvrdnji iz uvoda. Želimo imati realan broj u nazivniku, a znamo da je
u nazivniku, ali ne pretjerani problem - može nam poslužiti jedna od tvrdnji iz uvoda. Želimo imati realan broj u nazivniku, a znamo da je  uvijek realan, tako da broj
uvijek realan, tako da broj  možemo uvijek proširiti sa
možemo uvijek proširiti sa 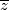 kako bismo mogli isčitati realni i imaginarni dio, ovdje nam treba
kako bismo mogli isčitati realni i imaginarni dio, ovdje nam treba 

 koji možete slobodno pokušati riješiti za vježbu. No, postoji bolji način za to riješiti.
koji možete slobodno pokušati riješiti za vježbu. No, postoji bolji način za to riješiti. je neki kompleksni broj
je neki kompleksni broj  , a svaki se može zapisati kao
, a svaki se može zapisati kao  , a mi znamo
, a mi znamo  te kada to uvrstimo imamo jednadžbu
te kada to uvrstimo imamo jednadžbu  koju rješavamo slično kao da imamo
koju rješavamo slično kao da imamo  u realnima, tako da sve invertiramo, tj. zamjenimo svemu brojnik i nazivnik te dalje možemo direktno dobiti
u realnima, tako da sve invertiramo, tj. zamjenimo svemu brojnik i nazivnik te dalje možemo direktno dobiti  za razliku od prvog primjera.
za razliku od prvog primjera. 
