MetaMath '24

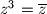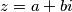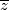\textit{Primjer. 3.} Odredite sve kompleksne brojeve $z$ za koje vrijedi $z^3=\overline{z}$. \textit{Rješenje.} Naravno, možemo opet probat $z=a+bi$ i opet bismo se napatili, ali opet imamo pametniji način uz jedan novi trik. S obzirom da je s jedne strane samo $z$, a s druge strane $\overline{z}$ htjeli bismo pomnožiti sve sa $z$ da dobijemo da je desna strana $\lvert z\rvert$, jer tada bismo saznali da je $z^4$ realan broj pa možemo samo korijenovat jednadžbu par puta da dobijemo (skoro) sva rješenja. 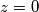Prvi problem je da ne smijemo uvijek množit sa $z$ jer što ako je $z=0$, ovdje se može uvrstiti i provjeriti da je 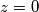$z=0$ stvarno jedno rješenje te sad smijemo množit sa $z$ uz pretpostavku $z\neq0$ u ostatku zadatka. Drugi problem je što trebamo zapravo odrediti $\lvert z\rvert$. Za kompleksan broj $z$ vrijedi $\lvert z\rvert=\lvert\overline{z}\rvert$ te $\lvert z^n\rvert=\lvert z\rvert^n$ a nitko nam ne brani da primjenimo modul na ovu jednadžbu i to ćemo i učiniti. Uz iznad navedena pravila imamo $$\lvert z^3\rvert=\lvert z\rvert^3=\lvert\overline{z}\rvert=\lvert z\rvert$$ odnosno $\lvert z\rvert^3=\lvert z\rvert$ što možemo prebaciti na jednu stranu faktorizirati kao $\lvert z\rvert(\lvert z\rvert^2-1)=0$. 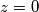Kako smo već komentirali slučaj $z=0$ i pretpostavili da je $z\neq0$ onda je i $\lvert z\rvert\neq0$ pa mora vrijediti $\lvert z\rvert^2=1$, a kako je modul uvijek nenegativan imamo $\lvert z\rvert=1$. Sada možemo pomnoćiti početnu jednadžbu sa $z$ te jednostavno primjeniti korijen par puta na sve slučajeve. \begin{align*} z^4=z\overline{z}&=\lvert z\rvert^2=1\quad/\sqrt{}\\ z^2=1&\quad z^2=-1\\ z_{1,2}=\pm1&\quad z_{3,4}=\pm\sqrt{-1}=\pm i \end{align*} Sada bismo trebali provjeriti jesu li to sva rješenja s obzirom da smo množili sa $z$, a to se lako provjeri. Dakle, sva rješenja su $0,\pm1,\pm i$. Kako biste dobili bod na ovom zadatku upišite 3 kao rješenje.