MetaMath '24

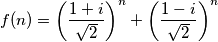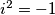Idući primjer je malo neobičan, ali svrha mu je spomenuti neke posebne kompleksne broj i trikove koji su specifični za njih. \textit{Primjer. 4.} Neka je $$f(n)=\left(\frac{1+i}{\sqrt{2}}\right)^n+\left(\frac{1-i}{\sqrt{2}}\right)^n$$ gdje je $n$ prirodan broj i $i^2=-1$. Odredite 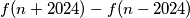$f(n+2024)-f(n-2024)$. \textit{Rješenje.} Ovaj zadatak izgleda malo ludo, znam, ali upravo zato je i ovdje jer je zapravo jako jednostavan ako se zna trik. E sad, taj trik nije ni zapravo trik, samo je lijepo svojstvo broja 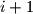$i+1$, naime 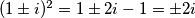$(1\pm i)^2=1\pm2i-1=\pm2i$, dakle 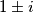$1\pm i$ se može vrlo jednostavno potencirati. Slično imamo za brojeve 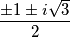$\dfrac{\pm1\pm i\sqrt{3}}{2}$ koji kad se kubiraju daju 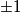$\pm1$ ovisno o predznacima. Stoga raspišimo 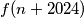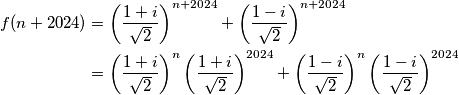$f(n+2024)$ \begin{align*} f(n+2024)&=\left(\frac{1+i}{\sqrt{2}}\right)^{n+2024}+\left(\frac{1-i}{\sqrt{2}}\right)^{n+2024}\\ &=\left(\frac{1+i}{\sqrt{2}}\right)^n\left(\frac{1+i}{\sqrt{2}}\right)^{2024}+\left(\frac{1-i}{\sqrt{2}}\right)^n\left(\frac{1-i}{\sqrt{2}}\right)^{2024} \end{align*} Kako je $$\left(\frac{1\pm i}{\sqrt{2}}\right)^{2024}=\left[\left(\frac{1\pm i}{\sqrt{2}}\right)^{2}\right]^{1012}=\left(\frac{\pm2i}{2}\right)^{1012}=(\pm i)^{2012}=1$$ zapravo je $f(n+2024)=f(n)$. 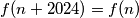Analogno se dobije 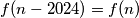$f(n-2024)=f(n)$ što ostavljam kao vježbu vama ;) Konačno, 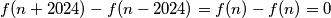$f(n+2024)-f(n-2024)=f(n)-f(n)=0$. Kako biste dobili bod na ovom zadatku kao rješenje upišite 4.